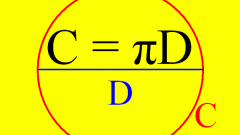Инструкция
1
Термин «длина» у большинства людей ассоциируется с соответствующей характеристикой прямой линии. Однако на самом деле, этот параметр имеется у линии любой формы. Так, например, она имеется у окружности.
2
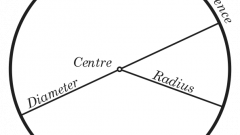
Окружность представляет собой замкнутый отрезок, который является образующей круга. Если точно следовать определению, то окружностью называется геометрическое место точек плоскости, равноудаленных от ее центра. Все окружности имеют некоторый радиус, обозначаемый как r, а также диаметр, равный D=2r. Длина этой линии равна значению выражения:C=2πr=πD, где r - радиус окружности, D - диаметр окружности.
3
Если речь идет о прямой линии, то имеется в виду либо обычный отрезок, либо замкнутая фигура, такая как треугольник или прямоугольник. Для последнего длина является основной характеристикой. Простой отрезок можно измерить экспериментально, а длину стороны у фигуры удобнее всего вычислить. Наиболее просто осуществить эту операцию в отношении прямоугольника.
4
Частным случаем прямоугольника является равносторонний, называемый квадратом. В условиях некоторых задач приведено только значение площади, а найти необходимо сторону. Поскольку стороны квадрата равны, то она вычисляется по следующей формуле:a = √S.Если прямоугольник не равносторонний, то, зная его площадь и одну из сторон, найдите длину перпендикулярной стороны следующим образом:a=S/b, где S - площадь прямоугольника, b - ширина прямоугольника.
5
Длина стороны треугольника находится несколько иным способом. Для определения этой величины необходимо знать не только длины остальных сторон, но и значения углов. Если дан прямоугольный треугольник с углом 60° и стороной с, которая является его гипотенузой, длину катета найдите по следующей формуле:a=c*cosα.Кроме того, если в задаче дана площадь треугольника и высота, длину основания можно найти по другой формуле:a=2√S/√√3.
6
Длину сторон любой фигуры проще всего найти, если она равносторонняя. Например, если вокруг равностороннего треугольника описана окружность, длину стороны этого треугольника вычислите следующим образом:a3=R√3.Для произвольного правильного n-угольника сторону найдите следующим образом:an=2R*sin(α/2)=2r*tg(α/2), где R - радиус описанной окружности, r - радиус вписанной окружности.