Как найти длину через массу

Масса определяется плотностью материала и объемом, которое занимает физическое тело в пространстве, поэтому обойтись одним лишь значением массы, увы, не получится. Если кроме нее доступны данные о материале пространственного объекта, то можно выяснить соответствующую ему плотность вещества. Тогда неизвестным останется лишь объем, одной из характеристик которого и является длина. Ниже приведены несколько способов определения длины для пространственных фигур правильной формы, при условии, что средняя плотность вещества известна.

Инструкция

1. Если пространственный объект имеет форму тора (цилиндра), то для определения его длины (L) необходимо знать площадь основания. Вычислить его можно, имея сведения о диаметре (d) тора. Если они есть, то используйте тот факт, что объем, с одной стороны равен отношению массы (m) к плотности (p), а с другой - четверти от произведения числа Пи на длину и возведенный в квадрат диаметр: m/p=¼*π*d²*L. Из этого тождества вытекает, что высота будет равна частному от деления учетверенной массы на произведение плотности на число Пи и квадрат диаметра: L=m*4/(p*π*d²).
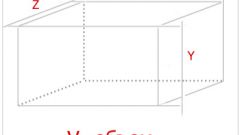
2. Если пространственная фигура представляет собой брус (прямоугольный параллелепипед) то площадь основания можно посчитать, зная ширину (w) и высоту (h), а если сечение имеет форму квадрата, то достаточно и одной стороны. В этом случае объем будет равен произведению длины на ширину и высоту и можно, как и на предыдущем шаге, составить тождество: m/p=w*h*L. Выведите из него значение высоты - она будет равна частному от деления массы на произведение плотности, ширины и высоты: L=m/(p*w*h).
3. Если объемная фигура имеет в сечении форму равностороннего треугольника, то для вычисления объема измерьте ширину одной грани (a), то есть сторону треугольника сечения. Площадь такого треугольника вычисляется умножением четверти от возведенной в квадрат длины стороны на квадратный корень из тройки, а для определения объема надо умножить результат на искомую длину (в данном случае ее правильнее назвать высотой). Вновь подставьте это значение в тождество: m/p=L*3*a²/4. Выведите из этого равенства формулу для вычисления длины - она будет представлять собой соотношение учетверенной массы и утроенного произведения плотности на квадрат стороны треугольника: L=4*m/(3*p*a²).