Инструкция
1
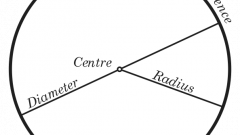
Например, чтобы найти длину окружности, достаточно определить в виде исходных данных известный диаметр. Задайте, что вам известен диаметр окружности, равный N, и начертите в соответствии с этими данными окружность. Поскольку диаметр соединяет две точки окружности и проходит при этом через центр, следовательно, радиус окружности всегда будет равен значению половинного диаметра, то есть r = N/2.
2
Используйте для нахождения длины либо любой другой величины математическую константу π. Она представляет собой отношение значения длины окружности к значению длины диаметра окружности и в геометрических вычислениях принимается равной π ≈ 3,14.
3
Чтобы определить длину окружности, возьмите стандартную формулу L = π*D и подставьте значение диаметра D = N. В результате диаметр, умноженный на величину 3.14, покажет приблизительную длину окружности.
4
В случае когда требуется определить не только длину окружности, но и ее площадь, также воспользуйтесь значением константы π. Только в этот раз воспользуйтесь другой формулой, согласно которой площадь круга определяется как длина радиуса, возведенная квадрат, и умноженная на число π. Соответственно формула выглядит следующим образом: S = π*(r^2).
5
Поскольку в исходных данных определено, что радиус r = N/2, следовательно, формула площади окружности видоизменяется: S = π*(r^2) = π*((N/2)^2). В результате, если вы подставите в формулу значение известного диаметра, вы получите искомую площадь.
6
Не забудьте проверить, в каких единицах измерения необходимо определить длину либо площадь окружности. Если в исходных данных определено, что диаметр измеряется в миллиметрах, площадь круга также должна измеряться в миллиметрах. Для других единиц - см2 или м2 расчеты производятся аналогично.