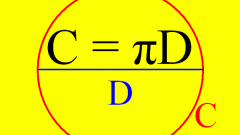Вам понадобится
- Величина радиуса окружности, диаметра, значение константы π.
Инструкция
1
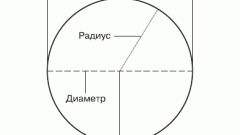
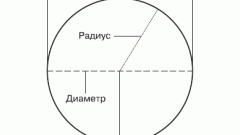
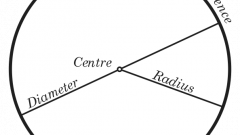
Сначала надо проанализировать исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова длина радиуса окружности. Вместо этого в задаче может быть дана длина диаметра окружности. Диаметр окружности - отрезок, который объединяет между собой две противоположные точки окружности, проходя через ее центр. Проанализировав определения окружности и диаметра, можно сказать, что длина диаметра равна удвоенной длине радиуса.
2
Теперь можно принять радиус окружности равным R. Тогда для нахождения длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L - длина окружности, D - диаметр окружности, который всегда в 2 раза больше радиуса.
L = 2πR = πD, где L - длина окружности, D - диаметр окружности, который всегда в 2 раза больше радиуса.
3
Можно рассмотреть пример применения данной формулы: дана окружность с диаметром 8 см. Требуется найти длину окружности.
Решение: L = 2*3,14*4 = 3,14*8 = 25,12 см
Ответ: длина окружности с диаметром 8 см равна 25,12 см
Решение: L = 2*3,14*4 = 3,14*8 = 25,12 см
Ответ: длина окружности с диаметром 8 см равна 25,12 см
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c - это стороны данного треугольника, S - площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c - это стороны данного треугольника, S - площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?