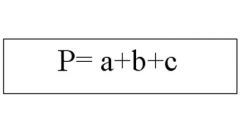Инструкция
1
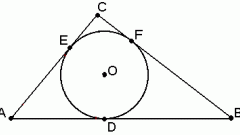
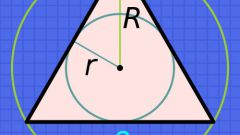
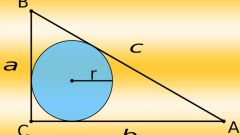
Начните вычисление длины вписанной в треугольник окружности (l) с определения ее радиуса (r). Если известна площадь многоугольника (S) и длины всех его сторон (a, b и c), то радиус будет равен отношению удвоенной площади к сумме этих длин r=2*S/(a+b+c).
2
Используйте геометрическое определение константы Пи для вычисления длины окружности по известному значению радиуса. Эта константа выражает отношение длины окружности к ее диаметру, то есть удвоенному радиусу. Значит, для нахождения длины окружности вам следует умножить полученное на предыдущем шаге значение радиуса на удвоенное число Пи. В общем виде эту формулу можно записать так: l=4*π*S/(a+b+c).
3
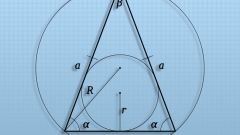
Если площадь треугольника неизвестна, но дана величина одного из его углов (α) и длины всех сторон (a, b и c), то радиус вписанной окружности (r) можно выразить через тангенс угла α. Для этого сначала сложите длины всех сторон и разделите результат пополам, потом отнимите от полученного значения длину той стороны (a), которая лежит напротив угла известной величины. Полученное число надо умножить на тангенс половины известной величины угла: r=((a+b+c)/2-a)*tg(α/2). Если этой формулой во втором шаге заменить выражение из первого шага, то формула длины окружности примет такой вид: l=2*π*((a+b+c)/2-a)*tg(α/2).
4
Можно обойтись и только длинами сторон треугольника (a, b и c). Но в этом случае для упрощения формулы лучше ввести дополнительную переменную - полупериметр треугольника: p=(a+b+c)/2. С ее помощью радиус вписанной окружности можно выразить как квадратный корень из частного от деления произведения разности полупериметра и длины каждой из сторон на полупериметр: r=√((p-a)*(p-b)*(p-c)/p). А формула длины вписанной окружности в этом случае приобретет такой вид: l=2*π*√((p-a)*(p-b)*(p-c)/p).
Видео по теме