Как найти центр вписанной окружности

Окружность может быть вписана в угол или в выпуклый многоугольник. В первом случае она касается обеих сторон угла, во втором — всех сторон многоугольника. Положение ее центра в обоих случаях вычисляется похожими способами. Необходимо провести дополнительные геометрические построения.

Вам понадобится

• - многоугольник;
• - угол заданного размера;
• - окружность с заданным радиусом;
• - циркуль;
• - линейка;
• - карандаш;
• - калькулятор.

Инструкция

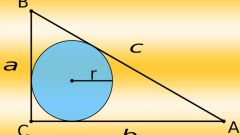
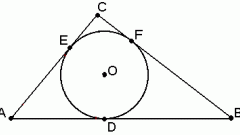
1. Найти центр вписанной окружности означает определить его положение относительно вершины отдельно взятого угла или углов многоугольника. Вспомните, где находится центр окружности, вписанной в угол. Он лежит на биссектрисе. Постройте угол заданного размера и разделите его пополам. Радиус вписанной окружности вы знаете. У вписанной окружности он же является и кратчайшим расстоянием от центра до касательной, то есть перпендикуляром. Касательной в данном случае является сторона угла. Постройте к одной из сторон перпендикуляр, равный заданному радиусу. Конечная его точка должна находиться на биссектрисе. У вас получился прямоугольный треугольник. Назовите его, например, ОСА. О — это вершина треугольника и одновременно центр окружности, ОС — радиус, а ОА — отрезок биссектрисы. Угол ОАС равен половине исходного угла. По теореме синусов найдите отрезок ОА, который является гипотенузой.
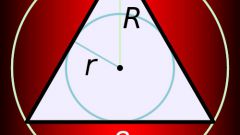
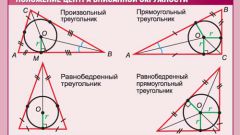
2. Для определения местоположения центра вписанной окружности в многоугольнике выполните аналогичные построения. Стороны любого многоугольника по определению являются касательными к вписанной окружности. Соответственно, радиус, проведенный к любой точке касания, будет ей перпендикулярен. В треугольнике центр вписанной окружности является точкой пересечения биссектрис, то есть расстояние его от углов определяется точно так же, как и в предыдущем случае.
3. Окружность, вписанная в многоугольник, одновременно является вписанной и в каждый его угол. Это следует из ее определения. Соответственно, расстояние центра от каждой из вершин можно вычислить точно так же, как и в случае с отдельно взятым углом. Это особенно важно помнить, если вы имеете дело с неправильным многоугольником. При вычислениях ромба или квадрата достаточно провести диагонали. Центр совпадет с точкой их пересечения. Определить его расстояние от вершин квадрата можно по теореме Пифагора. В случае с ромбом действует теорема синусов или косинусов, в зависимости от того, какой угол вы используете для вычислений.