Инструкция
1
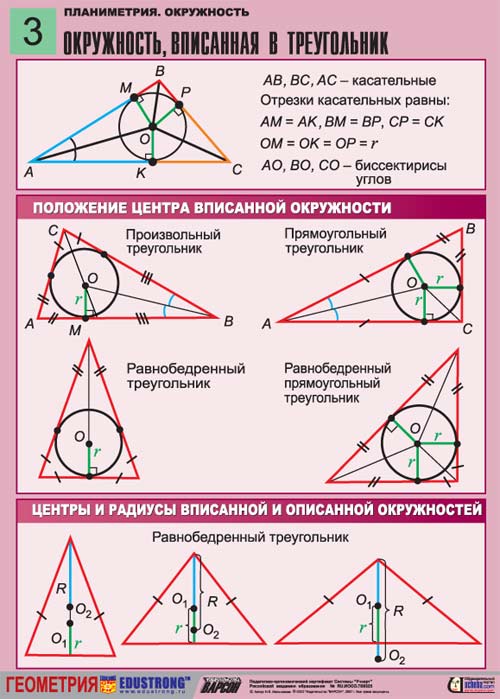
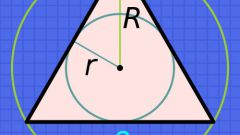
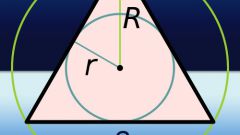
Представьте себе равнобедренный треугольник, в который вписана окружность неизвестного радиуса R. Поскольку окружность является вписанной в треугольник, а не описанной вокруг него, все стороны этого треугольника являются касательными к ней. Высота, проведенная из вершины одного угла перпендикулярно к основанию, совпадает с медианой этого треугольника. Она проходит через радиус вписанной окружности.
Следует отметить, что равнобедренным называется тот треугольник, у которого две боковые стороны равны. Углы при основании этого треугольника должны быть тоже равны. Такой треугольник, одновременно, можно вписать в окружность и описать около нее.
2
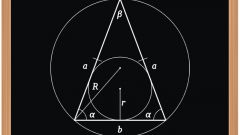
Сначала найдите неизвестное основание треугольника. Для этого, как уже сказано выше, проведите высоту из вершины треугольника к его основанию. Высота пересечет центр окружности. Если известна хотя бы одна из сторон треугольника, например, сторона CB, то вторая сторона ей равна, так как треугольник является равнобедренным. В данном случае, это - сторона AC. Третью сторону, которая является основанием треугольника, найдите по теореме Пифагора:
c^2=a^2+a^2-2a^2*cosy
Угол y между двумя равными сторонами найдите исходя из того, что в равнобедренном треугольнике два угла равны. Соответственно, третий угол равен y=180-(a+b).
3
Найдя все три стороны треугольника, перейдите к решению задачи. Формула, связывающая длины сторон и радиус, выглядит следующим образом:
r=(p-a)(p-b)(p-c)/p, где p=a+b+c/2 - сумма всех сторон, разделенных пополам, или полупериметр.
Если в окружность вписан равнобедренный треугольник, то в таком случае гораздо легче находить радиус окружности. При знании радиуса окружности, можно найти такие важные параметры, как площадь круга и длина окружности. Если в задании, наоборот, дан радиус окружности - это является, в свою очередь, предпосылкой к нахождению сторон треугольника. Найдя стороны треугольника, можно вычислить его площадь и периметр. Эти вычисления широко применяются во многих инженерных задачах. Планиметрия - это базовая наука, с помощью которой изучают более сложные геометрические вычисления.