Инструкция
1
Если длины всех сторон треугольника (a, b и c) известны, для вычисления радиуса (r) вписанной в него окружности придется извлекать квадратный корень. Но сначала добавьте к известным переменным еще одну - полупериметр (p). Рассчитайте его, сложив длины всех сторон и поделив результат пополам: p = (a+b+c)/2. Эта переменная значительно упростит общую формулу расчета. Формула должна состоять из знака радикала, под который помещена дробь с полупериметром в знаменателе. В числитель этой дроби поставьте произведение разностей полупериметра с длинами каждой из сторон: r = √((p-a)*(p-b)*(p-c)/p).
2
Знание площади треугольника (S) в дополнение к длинам всех сторон (a, b и c) позволит обойтись при вычислении радиуса вписанной окружности (r) без извлечения корня. Удвойте площадь и разделите результат на сумму длин всех сторон: r = 2*S/(a+b+c). Если и в этом случае ввести полупериметр (p = (a+b+c)/2), можно получить совсем простую формулу расчета: r = S/p.
3
Если в условиях даны длина одной из сторон треугольника (a), величина лежащего напротив него угла (α) и периметр (P), для вычисления радиуса вписанной окружности задействуйте одну из тригонометрических функций - тангенс. Формула расчета должна содержать разность между половиной периметра и длиной стороны, умноженную на тангенс половины величины угла: r = (P/2-a)*tg(α/2).
4
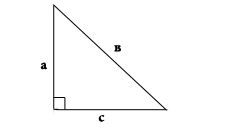
В прямоугольном треугольнике с известными длинами катетов (a, b) и гипотенузы (c) радиус вписанной окружности (r) вычисляется просто. Сложите длины катетов, вычтите из результата длину гипотенузы и поделите полученную величину пополам: r = (a+b-c)/2.
5
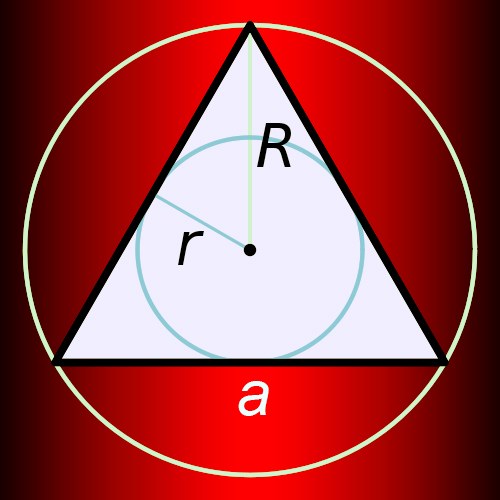
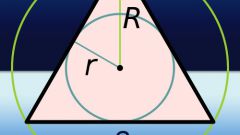
Радиус окружности (r), вписанной в правильный треугольник с известной длиной стороны (a) вычисляется по простой формуле. Правда, в ней присутствует бесконечная дробь, в числителе которой стоит корень из тройки, а в знаменателе - шестерка. На эту дробь умножьте длину стороны: r = a*√3/6.