Как построить описанную окружность?

Согласно определению, описанная окружность должна проходить через все вершины углов заданного многоугольника. При этом совершенно неважно, что это за многоугольник — треугольник, квадрат, прямоугольник, трапеция или что-то иное. Также не играет роли, правильный или неправильный это многоугольник. Необходимо лишь учитывать, что существуют многоугольники, вокруг которых окружность описать нельзя. Всегда можно описать окружность вокруг треугольника. Что касается четырехугольников, то окружность можно описать около квадрата или прямоугольника или равнобедренной трапеции.

Вам понадобится

• Заданный многоугольника
• Линейка
• Угольник
• Карандаш
• Циркуль
• Транспортир
• Таблицы синусов и косинусов
• Математические понятия и формулы
• Теорема Пифагора
• Теорема синусов
• Теорема косинусов
• Признаки подобия треугольников

Инструкция

1. Постройте многоугольник с заданными параметрами и определите, можно ли описать вокруг него окружность. Если вам дан четырехугольник, посчитайте суммы его противоположных углов. Каждая из них должна равняться 180°.
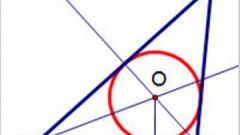
2. Для того, чтобы описать окружность, нужно вычислить ее радиус. Вспомните, где лежит центр описанной окружности в разных многоугольниках. В треугольнике он находится в точке пересечения всех высот данного треугольника. В квадрате и прямоугольники — в точке пересечения диагоналей, для трапеции- в точке пересечения оси симметрии к линии, соединяющей середины боковых сторон, а для любого другого выпуклого многоугольника — в точке пересечения серединных перпендикуляров к сторонам.
   
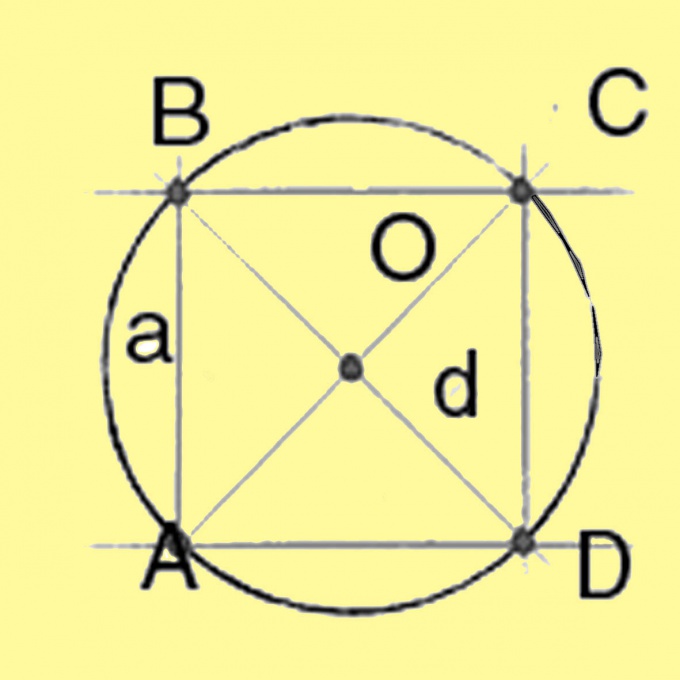
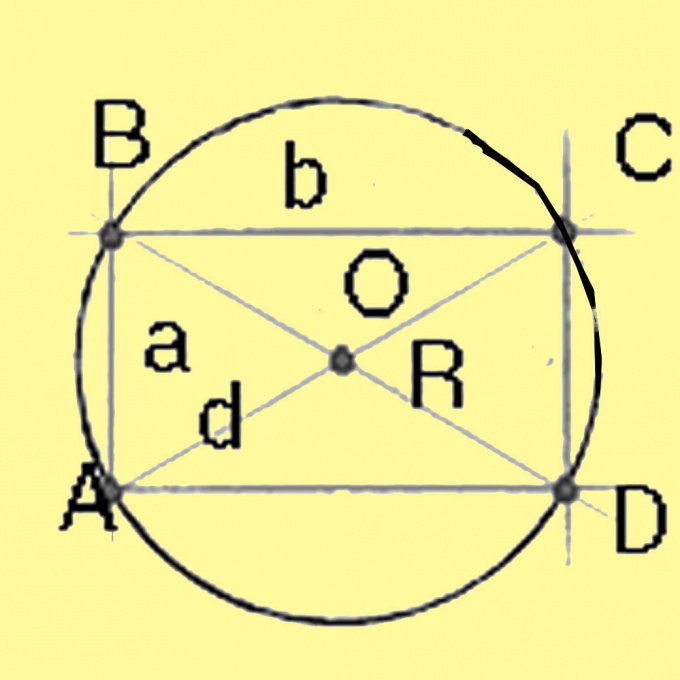
3. Диаметр окружности, описанной вокруг квадрата и прямоугольника, вычислите по теореме Пифагора. Он будет равняться квадратному корню из суммы квадратов сторон прямоугольника. Для квадрата, у которого все стороны равны, диагональ равна квадратному корню из удвоенного квадрата стороны. Разделив диаметр на 2, получаете радиус.
   
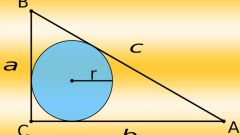
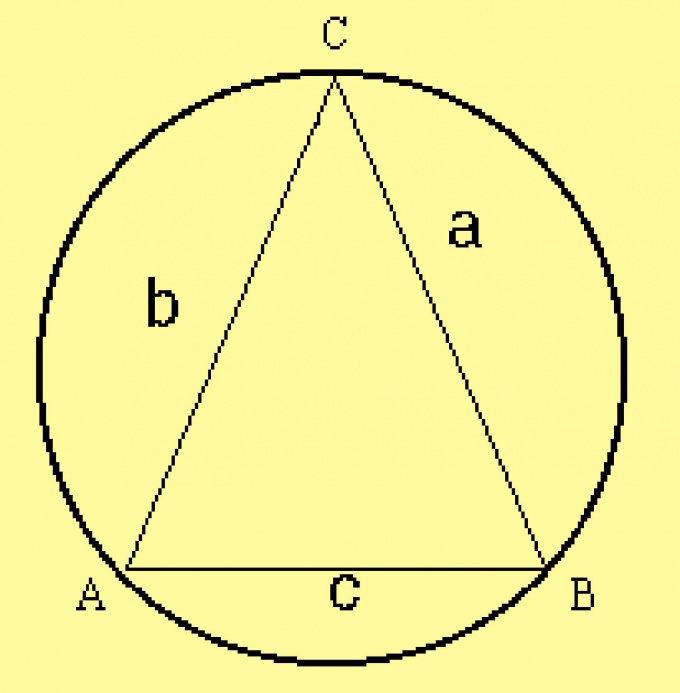
4. Вычислите радиус описанной окружности для треугольника. Поскольку параметры треугольника заданы в условиях, вычислите радиус по формуле R = a/(2·sinA), где а — одна из сторон треугольника, ? — противолежащий ей угол. Вместо этой стороны можно взять любую другую сторону и противолежащий ей угол.
   
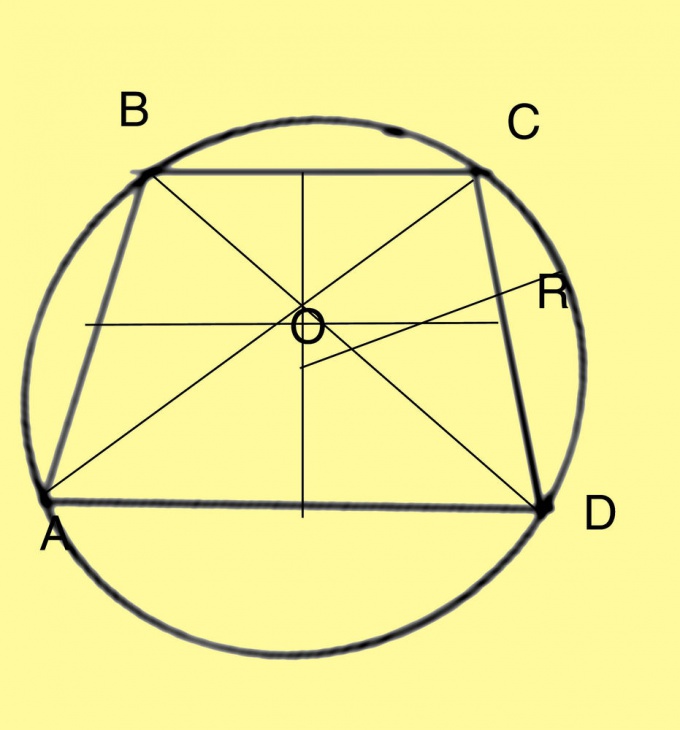
5. Вычислите радиус окружности, описанной вокруг трапеции.  R = a*d*c / 4 v(p*(p-a)*(p-d)*(p-c))   В этой формуле a и b — известные по условиям задания основания трапеции, h - высота, d - диагональ,  p = 1/2*(a+d+c) . Вычислите недостающие значения. Высоту можно вычислить по теореме синусов или косинусов, поскольку длины сторон трапеции и углы заданы в условиях задачи. Зная высоту и учитывая признаки подобия треугольников, вычислите диагональ. После этого останется только вычислить радиус по указанной выше формуле.