Как описать окружность около прямоугольного треугольника

Треугольник - простейшая из плоских многоугольных фигур. Если величина какого-либо угла в его вершинах равна 90°, то треугольник называется прямоугольным. Около такого многоугольника можно начертить круг таким способом, чтобы каждая из трех вершин имела одну общую точку с его границей (окружностью). Эта окружность будет называться описанной, а наличие прямого угла значительно упрощает задачу ее построения.

Вам понадобится

• Линейка, циркуль, калькулятор.

Инструкция

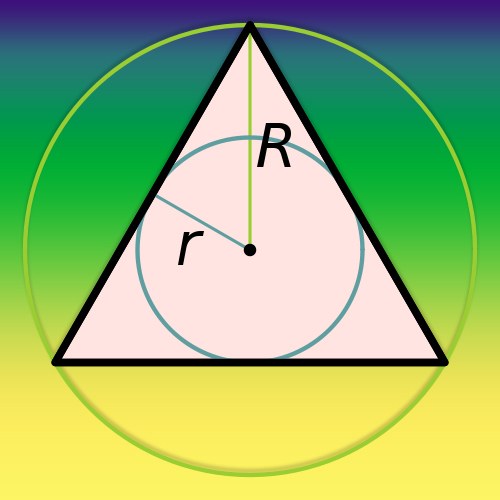
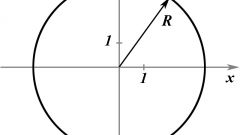
1. Начните с определения радиуса окружности, которую надо будет построить. Если есть возможность измерить длины сторон треугольника, то обратите внимание на его гипотенузу - сторону, лежащую напротив прямого угла. Измерьте ее и разделите полученное значение пополам - это и будет радиус описываемой около прямоугольного треугольника окружности.
2. Если длина гипотенузы неизвестна, но есть длины (a и b) катетов (двух сторон, прилегающих к прямому углу), то радиус (R) найдите с использованием теоремы Пифагора. Из нее вытекает, что этот параметр будет равен половине квадратного корня, извлеченного из суммы возведенных в квадрат длин катетов: R=½*√(a²+b²).
3. Если известна длина лишь одного из катетов (a) и величина прилегающего к нему острого угла (β), то для определения радиуса описанной окружности (R) используйте тригонометрическую функцию - косинус. В прямоугольном треугольнике она определяет соотношение длин гипотенузы и этого катета. Рассчитайте половину частного от деления длины катета на косинус известного угла: R=½*a/cos(β).
4. Если кроме длины одного из катетов (a) известна величина острого угла (α), лежащего напротив него, то для вычисления радиуса (R) воспользуйтесь другой тригонометрической функцией - синусом. Кроме замены функции и стороны в формуле ничего не изменится - разделите длину катета на синус известного острого угла, а результат поделите пополам: R=½*b/sin(α).
5. После нахождения радиуса любым из перечисленных способов определите центр описываемой окружности. Для этого отложите на циркуле полученное значение и установите его в любую вершину треугольника. Описывать полный круг нет необходимости, просто отметьте место его пресечения с гипотенузой - эта точка и будет центром окружности. Таково свойство прямоугольного треугольника - центр описанной около него окружности всегда находится в середине его самой длинной стороны. Начертите круг отложенного на циркуле радиуса с центром в найденной точке. На этом построение будет завершено.