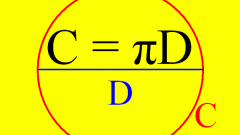Инструкция
1
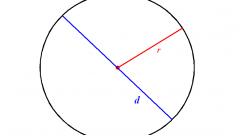
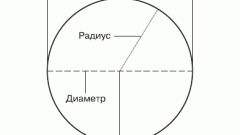
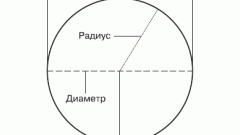
Найдите длину диаметра круга удвоением длины его радиуса, если эта длина известна. Это самый простой вариант исходных данных при необходимости определить длину диаметра.
2
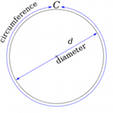
Используйте число Пи для нахождения длины диаметра по известной длине окружности. Эта константа выражает постоянное соотношение между этими двумя параметрами круга - независимо от размеров круга, деление длины его окружности на длину диаметра всегда дает одно и то же число. Из этого вытекает, что для нахождения длины диаметра следует длину окружности разделить на число Пи. Как правило, для практических вычислений длины диаметра бывает достаточно точности до сотых долей единицы, то есть до двух знаков после запятой, поэтому число Пи можно считать равным 3,14. Но так как эта константа является числом иррациональным, то имеет бесконечное число знаков после запятой. Если возникнет необходимость в более точном определении диаметра окружности, то нужное число знаков для числа пи можно найти, например, по этой ссылке - http://www.math.com/tables/constants/pi.htm.
3
При известной площади круга (S) для нахождения длины диаметра (d) удваивайте квадратный корень из отношения площади к числу Пи: d=2∗√(S/π).
4
При известной длине стороны описанного возле круга прямоугольника, длина диаметра будет равна этой известной величине.
5
При известных длинах сторон (a и b) прямоугольника, вписанного в круг, длину диаметра (d) можно вычислить, найдя длину диагонали этого прямоугольника. Поскольку диагональ здесь является гипотенузой в прямоугольном треугольнике, катеты которого образуют стороны известной длины, то по теореме Пифагора длину диагонали, а вместе с ней и длину диаметра описанной окружности, можно рассчитать, найдя квадратный корень из суммы квадратов длин известных сторон: d=√(a² + b²).