Инструкция
1
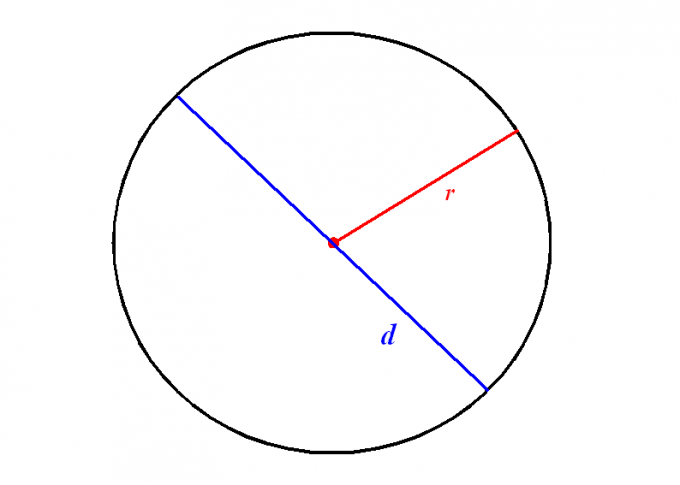
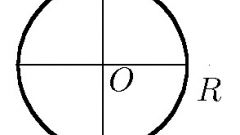
Отрезок, который соединяет любые две точки окружности, называется хордой.Проходящая через центр окружности хорда, называется ее диаметром. Диаметр обозначают символом или латинской буквой D. Диаметр (D) вдвое длиннее радиуса окружности (R) и является наибольшим возможным расстоянием между точками окружности.Пример. Радиус окружности равен 20 см. D(диаметр)-? Тогда, если R = 20 см, а мы знаем, что длина диаметра равна длине двух радиусов, то D = 2R = 2*20 = 40 см.
2
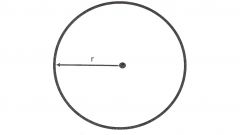
Есть второй способ найти диаметр окружности. В этом случае нам должна быть известна ее длина. Обозначьте длину окружности латинской буквой C. Пример. С = 60 см. D - ? Решение. Из геометрии мы знаем, что длина окружности находится по формуле: С = 2R, где: R – радиус окружности, а - иррациональное число «пи», равное приблизительно 3,14. Тогда, из этой формулы следует другая: D = С : 3,14. Значит, D = 60 : 3,14 = 19,12 см.
Полезный совет
Окружность иногда называют «колесом геометрии». Одно из свойств колеса – его ось остается все время на неизменном расстоянии от поверхности, по которой оно катится - в математической формулировке превращается в определение окружности. Окружностью называют множество точек плоскости, удаленных от некоторой точки, ее центра, на одно и то же расстояние, или радиус (от латинского radius – «спица колеса», «луч»). Радиусами называются также отрезки, соединяющие центр с точками окружности.
Диаметр делит окружность на равные части. Комментатор «Начал» древнегреческий философ Прокл, живший в V веке, приписывал это открытие Фалесу, признанному родоначальником античной философии и науки. Уточняя данное утверждение, можно сказать, что окружность симметрична относительно любого своего диаметра (точнее, содержащей его прямой).*
* Энциклопедия для детей, том 11 «Математика», Москва «Аванта+», 1998г.
Диаметр делит окружность на равные части. Комментатор «Начал» древнегреческий философ Прокл, живший в V веке, приписывал это открытие Фалесу, признанному родоначальником античной философии и науки. Уточняя данное утверждение, можно сказать, что окружность симметрична относительно любого своего диаметра (точнее, содержащей его прямой).*
* Энциклопедия для детей, том 11 «Математика», Москва «Аванта+», 1998г.