Вам понадобится
- Чертеж с треугольником, транспортир, циркуль, линейка, карандаш.
Инструкция
1
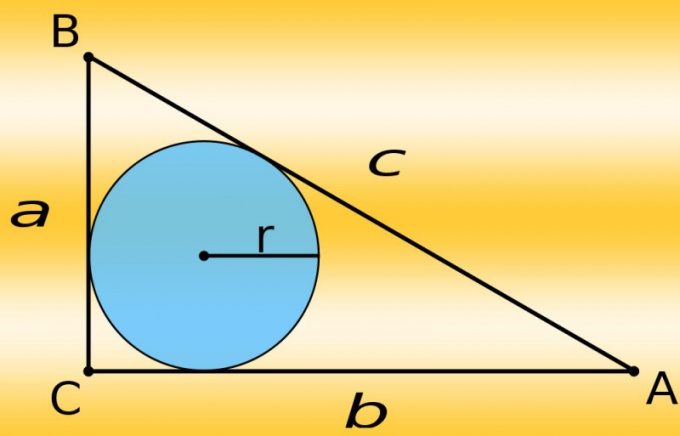
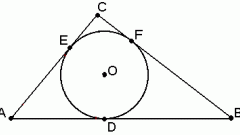
Найдите точку, которая будет центром вписанной окружности. Она должна лежать на пересечении биссектрис углов в вершинах треугольника, поэтому сначала приложите транспортир к одному из углов, определите его величину и поставьте вспомогательную точку на отметке, равной половине этой величины. Проведите отрезок из вершины этого угла - он должен пройти через вспомогательную точку и закончиться на противолежащей стороне. Таким же способом постройте биссектрису другого угла. Точка пересечения двух вспомогательных отрезков будет центром вписанной окружности.
2
Определите радиус круга. Для этого проведите еще один вспомогательный отрезок. Он должен начинаться в найденной точке, заканчиваться на одном из катетов и быть параллельным другому катету. Длина этого отрезка и будет радиусом вписанной окружности - отложите ее на циркуле и начертите круг с центром в найденной точке. На этом построение будет завершено.
3
Можно начертить вписанную окружность по-другому - с использованием формулы из курса элементарной геометрии. Для этого вам нужно знать длины всех сторон - измерьте их. Затем рассчитайте радиус (r) - сложите длины катетов (a и b), отнимите от результата длину гипотенузы (c), а то, что получилось, поделите пополам: r = (a+b-c)/2. Отложите найденную величину на циркуле и до конца построения не меняйте этого расстояния.
4
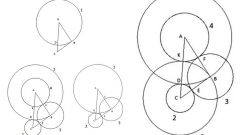
Установите циркуль в вершину прямого угла и начертите вспомогательную дугу - она должна пересекать оба катета. Собственно, только точки пересечения вам и нужны, поэтому вместо дуги можно просто поставить метки на катетах. Эти метки указывают точки касания вписанной окружности и сторон треугольника.
5
Установите циркуль в каждую из точек касания и проведите два полукруга, лежащих внутри треугольника. Точка их пересечения будет центром вписанной окружности - установите в нее циркуль и проведите вписанный в прямоугольный треугольник круг.
Источники:
- Как найти радиус вписанной в треугольник окружности?