Инструкция
1
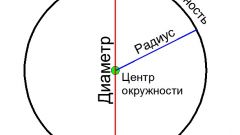
Окружностью называется геометрическое место точек, равноудаленных от центра. Она является замкнутой кривой, у которой все точки постоянны. Окружность составляет основу круга. Разрежьте батон колбасы - и получатся равные по длине круги. Соответственно, пленка, являющаяся окантовкой батона, окажется разрезанной на окружности. Круг является также сечением шара. Для получения самого большого из них рассеките шар в середине. Он проходит через центр шара и имеет максимальную длину окружности.
2
Начертите шар с некоторым диаметром, равным D. Проведите сечение строго по его центру, в результате чего получится круг с диаметром, равным диаметру шара. Вращая этот круг вокруг своей оси, получите шар того же диаметра, что и первоначальный. Если же вращать не круг, а окружность, вместо шара получится полая фигура, называемая сферой. Чтобы вычислить длину круга в данном примере, необходимо рассчитать длину окружности. Численно этот параметр равен длине окружности. Вычислите ее, пользуясь приведенной ниже формулой:C=πD=2πR.Такой способ решения задачи применяется только тогда, когда известны радиус или диаметр круга. Однако на практике в учебниках по геометрии встречаются задачи о кругах, требующие многоэтапного решения.
3
Начертите конус, у которого сечение проведено через середину высоты параллельно основанию. Высота его равна h, а длина образующей составляет l. Из полученного вами чертежа видно, что для того, чтобы найти радиус круга, образовавшегося в результате сечения конуса плоскостью, необходимо применить стандартную теорему Пифагора. Поскольку сечение проведено в середине конуса, то длина высоты равна h/2, а длина образующей составит l/2. Соответственно, по теореме Пифагора найдите радиус по формуле показанной ниже:R=√(l/2)^2-(h/2)^2.Отсюда следует, что длина данной окружности может быть вычислена следующим образом:С=2πR=2π√(l/2)^2-(h/2)^2.
Видео по теме