Вам понадобится
- - угольник;
- - линейка.
Инструкция
1
Простейший способ найти центр окружности – согнуть листок бумаги, на котором она начерчена, убедившись, глядя на просвет, что она сложилась точно пополам. Затем согните лист перпендикулярно первому сгибу. Так вы получите диаметры, точка пересечения которых и есть центр фигуры.
2
Конечно, этот способ идеален, только если окружность начерчена на бумаге, достаточно тонкой, чтобы можно было посмотреть на просвет, точно ли сложен лист.
3
Допустим, рассматриваемую фигуру начертили на твердой, несгибаемой поверхности либо это отдельная деталь, которая также не поддается сгибу. Чтобы найти центр окружности в этом случае, вам нужна линейка.
4
Диаметр является самым длинным отрезком, соединяющим 2 точки окружности. Как известно, проходит он через центр, поэтому задача нахождения центра окружности сводится к нахождению диаметра и его середины.
5
Наложите линейку на окружность, после чего зафиксируйте в любой точке фигуры нулевую отметку. Приложите линейку к окружности, получив секущую, а затем двигайте по направлению к центру фигуры. Длина секущей будет возрастать, пока не дойдет до пиковой точки. Вы получите диаметр, а найдя его середину, найдете и центр окружности.
6
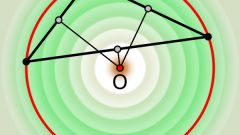
Центр описанной окружности для любого треугольника располагается на пересечении срединных перпендикуляров. В случае, если треугольник прямоугольный, ее центр всегда будет совпадать с серединой гипотенузы. То есть решение кроется в построении внутри окружности прямоугольного треугольника с вершинами, лежащими на окружности.
7
Трафаретом для прямого угла могут послужить школьный или строительный угольник, линейка или даже лист бумаги/картона. Поместите в любую точку окружности вершину прямого угла, сделайте отметки в тех местах, где стороны угла пересекают границу окружности, соедините их. У вас получился диаметр – гипотенуза.
8
Таким же способом найдите еще один диаметр, место пересечения двух таких отрезков и будет центром окружности.
Видео по теме