Инструкция
1
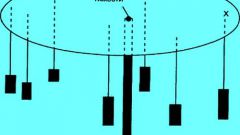
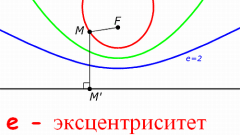
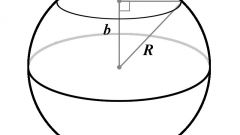
Рассмотрите простейший рычаг (см. рис 1), находящийся в положении равновесия. Расположите точку опоры на горизонтальной оси с абсциссой х₁₂ и поместите на краях материальные точки масс m₁ и m₂. Считайте их координаты по оси 0х известными и равными х₁ и х₂. Рычаг находится в положении равновесия, если моменты сил веса Р₁=m₁g и P₂=m₂g равны. Момент равен произведению силы на ее плечо, которое можно найти как длину перпендикуляра опущенного из точки приложения силы на вертикаль х=х₁₂. Поэтому, в соответствии с рисунком 1, m₁gℓ₁= m₂gℓ₂, ℓ₁=х₁₂-х₁, ℓ₂=х₂-х₁₂. Тогда m₁(х₁₂-х₁)=m₂(х₂-х₁₂). Решите это уравнение и получите х₁₂=(m₁x₁+m₂x₂)/(m₁+m₂).
2
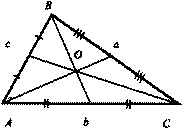
Для выяснения ординаты центра тяжести y₁₂ примените те же самые рассуждения и выкладки, как и на шаге 1. По-прежнему следуйте иллюстрации, приведенной на рисунке 1, где m₁gh₁= m₂gh₂, h₁=y₁₂-y₁, h₂=y₂-y₁₂. Тогда m₁(y₁₂-y₁)=m₂(y₂-y₁₂). Результат - у₁₂=(m₁у₁+m₂у₂)/(m₁+m₂). Далее считайте, что вместо системы из двух точек имеется одна точка М₁₂(x12,у12) общей массы (m₁+m₂).
3
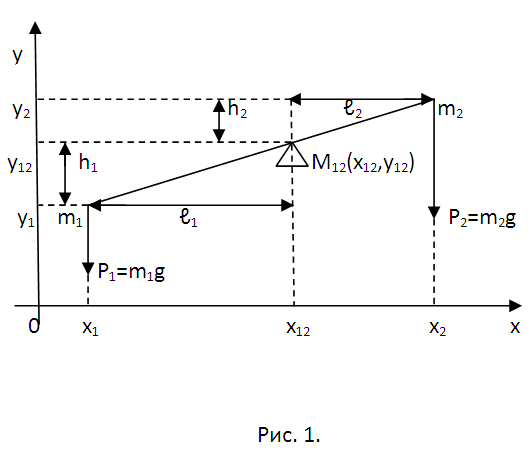
К системе из двух точек добавьте еще одну массу (m₃) с координатами (х₃, у₃). При вычислении следует по-прежнему считать, что имеете дело с двумя точками, где вторая из них имеет массу (m₁+m₂) и координаты (x12,у12). Повторяя уже для этих двух точек все действия шагов 1 и 2, придете к координатам центра тяжести системы трех точек x₁₂₃=(m₁x₁+m₂x₂+m₃x₃)/(m₁+m₂+m₃), у₁₂₃=(m₁у₁+m₂у₂+m₃y₃)/(m₁+m₂+m₃). Далее добавляйте четвертую, пятую и так далее точки. После многократного повторения все той же процедуры убедитесь, что для системы n точек координаты центра тяжести вычисляются по формуле (см. рис. 2). Отметьте для себя тот факт, что в процессе работы ускорение свободного падения g сокращалось. Поэтому координаты центра масс и тяжести совпадают.
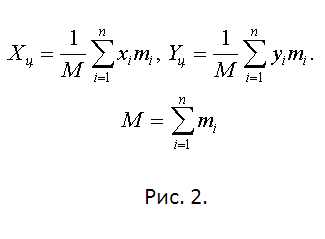
4
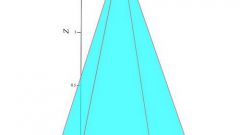
Представьте себе, что в рассматриваемом сечении расположена некоторая область D, поверхностная плотность которой ρ=1. Сверху и снизу фигура ограничена графиками кривых у=φ(х) и у=ψ(х), х є [а,b]. Разбейте область D вертикалями x=x₍i-1₎, x=x₍i₎ (i=1,2,…,n) на тонкие полоски, такие, что их можно приблизительно считать прямоугольниками с основаниями ∆хi (см. рис. 3). При этом середину отрезка ∆хi считайте положите совпадающим с абсциссой центра масс ξi=(1/2)[xi+x(i-1)]. Высоту прямоугольника считайте приблизительно равной [φ(ξi)-ψ(ξi)]. Тогда ордината центра масс элементарной площади ηi=(1/2)[φ(ξi)+ψ(ξi)].
5
В силу равномерного распределения плотности считайте, что центр масс полоски совпадет с ее геометрическим центром. Соответствующая элементарная масса ∆mi=ρ[φ(ξi)-ψ(ξi)]∆хi=[φ(ξi)-ψ(ξi)]∆хi сосредоточена в точке (ξi,ηi). Наступил момент обратного перехода от массы, представленной в дискретной форме, к непрерывной. В соответствии с формулами вычисления координат (см. рис. 2) центра тяжести образуются интегральные суммы, проиллюстрированные на рисунке 4а. При предельном переходе при ∆xi→0 (ξi→xi) от сумм к определенным интегралам, получите окончательный ответ (рис. 4b). В ответе масса отсутствует. Равенство S=M следует понимать лишь как количественное. Размерности здесь отличны друг от друга.
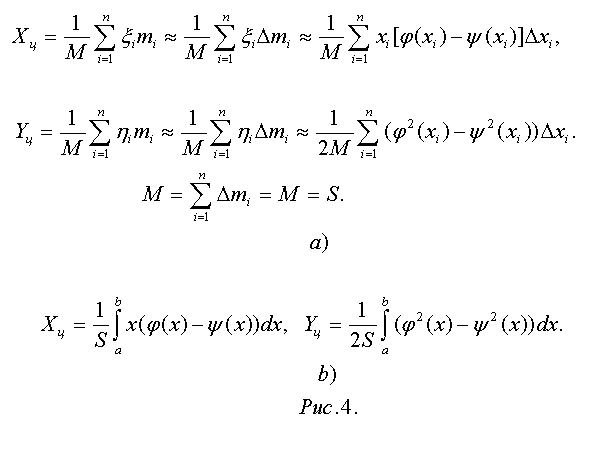
Источники:
- Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1., М.: 1978, 456 с., ил.