Как найти натуральную величину треугольника

Геометрическая фигура может быть изображена вращающейся, то есть занимающей определенное положение по отношению к неподвижной системе плоскостей проекции. В качестве оси вращения может использоваться любая прямая. Зная исходные данные вращающейся фигуры, можно определить ее натуральную величину, а также найти расстояние от заданной точки до треугольника.

Вам понадобится

• - учебник «Геометрия»;
• - линейка;
• - простой карандаш;
• - тетрадь.

Инструкция

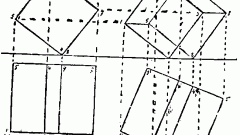
1. Решите данную задачу путем замены плоскостей проекции. Прямые плоскости, проходящие перпендикулярно к линиям уровня данной плоскости, в геометрии получили название линий наибольшего наклона плоскости к соответствующей ей плоскости проекций. Проведите на рисунке горизонталь h и фронталь f. Ввиду того, что линия наибольшего наклона плоскости является перпендикулярной плоскости проекции П1 (эта перпендикулярность сохранена на горизонтальной проекции), ее горизонтальная проекция будет проходить через точку С1, то есть перпендикулярно проекции h1. Поскольку линия наибольшего наклона перпендикулярна к проекции плоскости П2, фронтальная проекция треугольника должна быть перпендикулярна проекции f2.
   
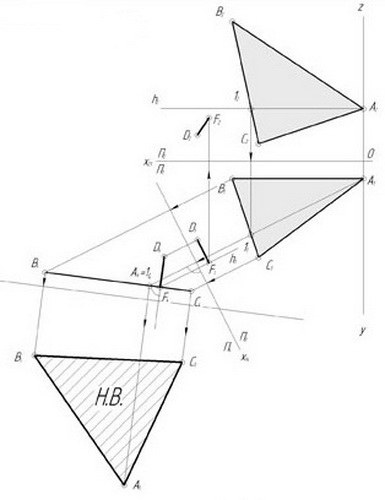
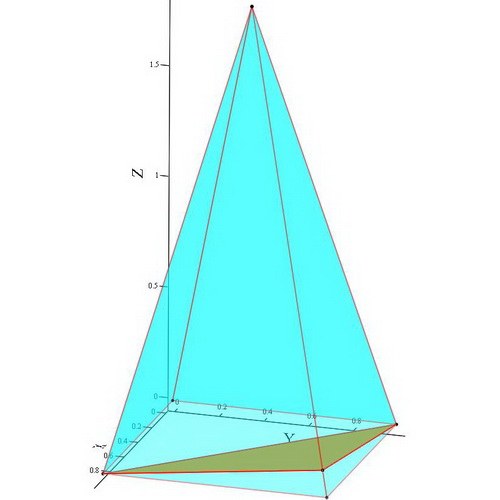
2. Для того чтобы преобразовать проецирующую плоскость в плоскость уровня, постройте еще одну плоскость проекций: она должна располагаться параллельно проекции треугольника с вершинами А4, В4 и С4. Затем проведите связующие линии и отложите координаты точек, которые взяты из плоскости П1. Полученная на рисунке проекция треугольника А5В5С5 будет соответствовать натуральной величине треугольника АВС.
3. Найдя натуральную величину треугольника ABC, с легкостью сможете определить расстояние от некой точки D до треугольника. Для этого опустите перпендикуляр из точки D на плоскость той проекции, которая является проецирующей. После этого найдите длину опущенного перпендикуляра.