Инструкция
1
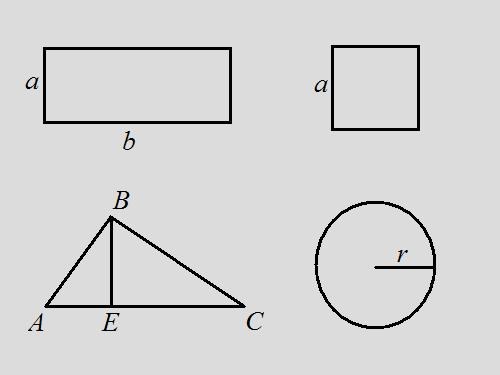
ПрямоугольникЗадача: найдите периметр прямоугольника, если известно, что площадь равна 18, а длина прямоугольника в 2 раза больше ширины.Решение: запишите формулу площади для прямоугольника – S = a*b. По условию задачи b = 2*a, отсюда 18 = a*2*a, a = √9 = 3. Очевидно, что b = 6. По формуле периметр равен сумме всех сторон прямоугольника – P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18. В данной задаче периметр совпал по значению с площадью фигуры.
2
КвадратЗадача: найдите периметр квадрата, если его площадь равна 9.Решение: по формуле площади квадрата S = a^2, отсюда найдите длину стороны a = 3. Периметр равен сумме длин всех сторон, следовательно, P = 4*a = 4*3 = 12.
3
ТреугольникЗадача: дан произвольный треугольник ABC, площадь которого равна 14. Найдите периметр треугольника, если проведенная из вершины B высота делит основание треугольника на отрезки длиной 3 и 4 см.Решение: по формуле площадь треугольника – это половина произведения основания на высоту, т.е. S = ½*AC*BE. Периметр равен сумме длин всех сторон. Длину стороны AC найдите, сложив длины AE и EC, AC = 3 + 4 = 7. Найдите высоту треугольника BE = S*2/AC = 14*2/7 = 4.Рассмотрите прямоугольный треугольник ABE. Зная катеты AE и BE, можно найти гипотенузу по формуле Пифагора AB^2 = AE^2 + BE^2, AB = √(3^2 + 4^2) = √25 = 5.Рассмотрите прямоугольный треугольник BEC. По формуле Пифагора BC^2 = BE^2 + EC^2, BC = √(4^2 + 4^2) = 4*√2.Теперь известны длины всех сторон треугольника. Найдите периметр из их суммы P = AB + BC + AC = 5 + 4*√2 + 7 = 12 + 4*√2 = 4*(3+√2).
4
ОкружностьЗадача: известно, что площадь окружности равна 16*π, найдите ее периметр.Решение: запишите формулу площади окружности S = π*r^2. Найдите радиус окружности r = √(S/π) = √16 = 4. По формуле периметр P = 2*π*r = 2*π*4 = 8*π. Если принять, что π = 3.14, то P = 8*3.14 = 25.12.