Инструкция
1
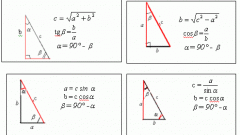
Зная периметр и сторону фигуры, можно найти другую ее сторону, а также площадь. Сам же периметр, в свою очередь, может быть найден по нескольким заданным сторонам либо по углу и сторонам, в зависимости от условий задачи. Также в ряде случаев его выражают через площадь. Наиболее просто находится периметр прямоугольника. Начертите прямоугольник с одной из сторон, равной а, и диагональю, равной d. Зная эти две величины, найдите по теореме Пифагора другую его сторону, которая является шириной прямоугольника. Найдя ширину прямоугольника, вычислите его периметр следующим образом: p=2(a+b). Эта формула справедлива для всех прямоугольников, поскольку у любого из них четыре стороны.
2
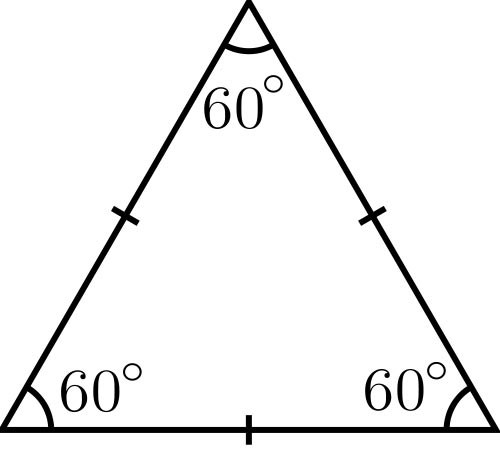
Обратите внимание на тот факт, что периметр треугольника в большинстве задач находят при наличии информации хотя бы об одном его угле. Однако, имеются и задачи, в которых все стороны треугольник известны, и тогда периметр может быть вычислен простым суммированием, без использования тригонометрических вычислений: p=a+b+c, где a, b и c - стороны. Но такие задачи встречаются в учебниках редко, поскольку способ их решения очевиден. Более сложные задачи по нахождению периметра треугольника решайте поэтапно. Например, начертите равнобедренный треугольник, у которого известны основание и угол при нем. Для того чтобы найти его периметр, вначале найдите стороны a и b следующим образом: b=c/2cosα. Поскольку a=b (треугольник равнобедренный), сделайте следующий вывод: a=b=c/2cosα.
3
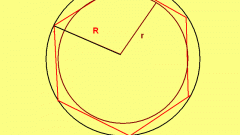
Периметр многоугольника вычисляйте аналогичным образом, складывая длины всех его сторон: p=a+b+c+d+e+f и так далее. Если многоугольник правильный и вписан в окружность или описан около нее, вычислите длину одной из его сторон, а затем умножьте на их количество. Например, чтобы найти стороны шестиугольника, вписанного в окружность, действуйте следующим образом: a=R, где a - сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник правильный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r√3/3. Соответственно, периметр такой фигуры найдите следующим образом: p=12r√3/3.