Вам понадобится
  • - ручка;
  • - бумага для записей.
Инструкция
1
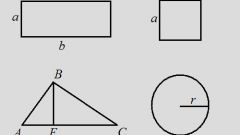
Периметр прямоугольника вы можете найти, сложив длины всех его сторон. Так как у прямоугольника противолежащие стороны равны, периметр можно задать формулой: p = 2(a+b), где а, b – прилежащие стороны.
2
Пример задачи: в условии сказано, что одна сторона прямоугольника имеет длину 12 см, а вторая в три раза ее меньше. Требуется найти периметр.
3
Для решения рассчитайте длину второй стороны: b = 12/3 = 4 cм. Периметр прямоугольника будет равен: 2(4+12) = 32 см.
4
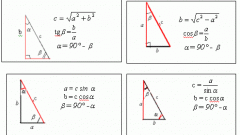
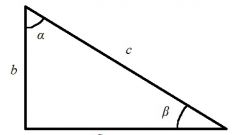
Третий пример – в задаче даны только длина одной стороны и диагональ. Треугольник, образованный двумя сторонами и диагональю – прямоугольный. Найдите вторую сторону из уравнения Пифагора: b = (c^2-a^2)^1/2. Затем вычислите периметр по формуле из шага 1.
5
Четвертый пример – задана длина диагонали и угол между диагональю и стороной прямоугольника. Рассчитайте длину стороны из выражения: b = sina*c, где b – противолежащая углу сторона прямоугольника, с – его диагональ. Найдите прилежащую к углу сторону: a = cosa*c. Зная длины сторон, определите периметр.
6
Пятый пример – прямоугольник вписан в окружность с известным радиусом. Центр окружности лежит в точке пересечения серединных перпендикуляров многоугольника. Для прямоугольника это совпадает с точкой пересечения его диагоналей. Значит, длина диагонали равна диаметру окружности или двум радиусам. Далее, в зависимости от условий задачи, найдите стороны многоугольника аналогично шагу 2 или 3.
7
Шестой пример: чему равен периметр прямоугольника, если его площадь – 32 см2? Известно также, что одна его сторон в два раза больше другой.
8
Площадь прямоугольника – это произведение двух его прилежащих сторон. Обозначьте длину одной стороны за x. Вторая будет равна 2х. У вас получилось уравнение: 2x*x = 32. Решив его, найдите х = 4 см. Найдите вторую сторону – 8 см. Вычислите периметр: 2(8+4) = 24 см.