Вам понадобится
- - линейка или рулетка;
- - прочная нить;
- - роликовый дальномер.
Инструкция
1
2
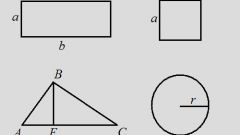
Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр обычной веревкой или ниткой. Для этого расположите ее так, чтобы она точно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если можно, просто обрежьте ее чтобы избежать путаницы. Затем при помощи рулетки или линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Обязательно следите за тем, чтобы нить максимально точно повторяла линию для большей точности результата.
3
Периметр сложной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в исходную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.
4
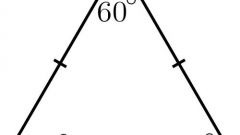
Периметр некоторых геометрических фигур вычисляйте. Например, чтобы найти периметр любого правильного многоугольника (выпуклого многоугольника, стороны которого равны), длину стороны умножьте на количество углов или сторон (они равны). Чтобы найти периметр правильного треугольника со стороной 4 см умножьте это число на 3 (Р=4∙3=12 см).
5
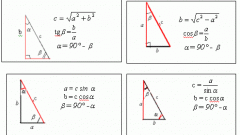
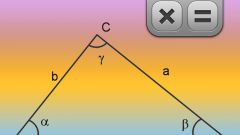
Чтобы найти периметр произвольного треугольника, сложите длины всех его сторон. Если не даны все стороны, а есть углы между ними, найдите их по теореме синуса или косинуса. Если известны две стороны прямоугольного треугольника, третью найдите по теореме Пифагора и найдите их сумму. Например, если известно, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна √(3²+4²)=5 см. Тогда периметр Р=3+4+5=12 см.
6
Чтобы найти периметр круга, найдите длину окружности, которая его ограничивает. Для этого ее радиус r умножьте на число π≈3,14 и число 2 (P=L=2∙π∙r). Если известен диаметр, учитывайте, что он равен двум радиусам.
Источники:
- периметру