Инструкция
1
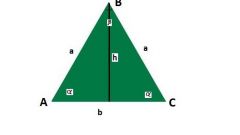
Если все три стороны треугольника уже даны в условии задачи, просто сложите их. Тогда периметр будет равен: P = a + b + c.
2
Пусть даны две стороны a, b и угол между ними γ. Тогда третью сторону можно найти по теореме косинусов: c² = a² + b² - 2 • a • b • cos(γ). Помните, что длина стороны может быть только положительной.
3
Частный случай теоремы косинусов – теорема Пифагора, которая применима для прямоугольных треугольников. Угол γ в данном случае равен 90°. Косинус прямого угла обращается в единицу. Тогда c² = a² + b².
4
Если в условии дана только одна из сторон, но при этом известны углы треугольника, две другие стороны можно найти по теореме синусов. Кстати, углы могут быть заданы не все, поэтому полезно помнить, что сумма всех углов треугольника равна 180°.
5
Итак, пусть дана сторона a, угол γ между a и b, β между a и c. Третий угол α между сторонами b и c легко найти из теоремы о сумме углов треугольника: α = 180° - β – γ. По теореме синусов, a / sin(α) = b / sin(β) = c / sin(γ) = 2 • R, где R – радиус окружности, описанной около треугольника. Чтобы найти сторону b, можно выразить ее из этого равенства через углы и сторону a: b = a • sin(β) / sin(α). Аналогично выражается и сторона c: c = a • sin(γ) / sin(α). Если, например, дан радиус описанной окружности, но не дана длина ни одной из сторон, задачу также возможно решить.
6
Если в задаче дана площадь фигуры, надо записать формулу для площади треугольника через стороны. Выбор формулы зависит от того, что еще известно. Если, помимо площади, заданы две стороны, поможет применение формулы Герона. Площадь можно выразить также через две стороны и синус угла между ними: S = 1/2 • a • b • sin(γ), где γ – угол между сторонами a и b.
7
В некоторых задачах может быть задана площадь и радиус окружности, вписанной в треугольник. В таком случае выручит формула r = S / p, где r – радиус вписанной окружности, S – площадь, p – полупериметр треугольника. Полупериметр из этой формулы выразить легко: p = S / r. Осталось найти периметр: P = 2 • p.