Инструкция
1
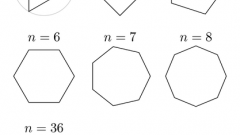
В самом простом случае, когда известны длина стороны (а) правильного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) просто перемножьте эти две величины: Р = а*n. Например, длина периметра правильного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.
2
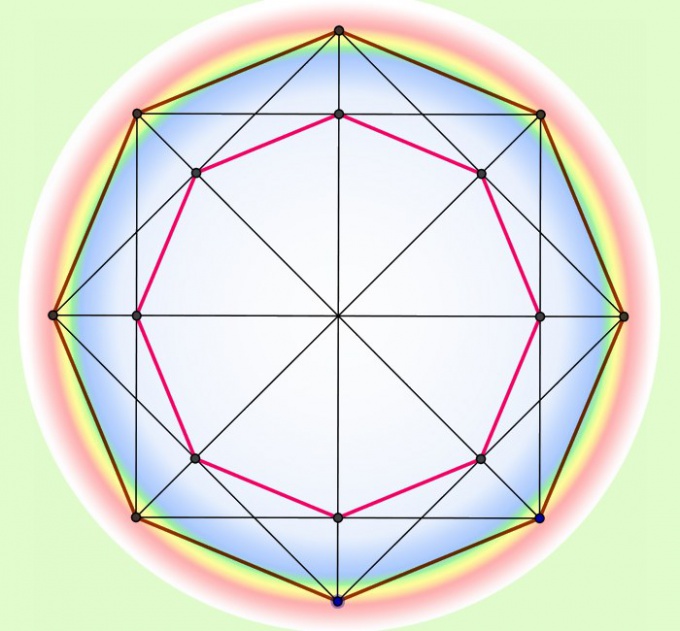
Вычислить периметр такого многоугольника по известному радиусу (R) описанной около него окружности тоже возможно. Для этого придется сначала выразить длину стороны с использованием радиуса и количества вершин (n), а затем умножить полученную величину на число сторон. Чтобы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на количество вершин, а результат удвойте: R*sin(π/n)*2. Если вам удобнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(π/n)*2*n = R*sin(180°/n)*2*n. Например, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.
3
Схожим способом можно посчитать периметр, не зная длины стороны правильного многоугольника, если он описан около окружности с известным радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, чтобы получить такое выражение: r*tg(π/n)*2. Или для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное количеству вершин многоугольника: Р = r*tg(π/n)*2*n = r*tg(180°/n)*2*n. Например, периметр восьмиугольника, описанного возле круга с радиусом в 40 см, будет приблизительно равен 40*tg(180°/8)*2*8 ≈ 40*0,414*16 = 264,96 см.