Инструкция
1
Для квадрата периметр (P) равен четырехкратному значению одной его стороны (b). P = 4*b или сумме значений длин всех его сторон P = b + b + b + b. Площадь квадрата выражается в произведении двух смежных сторон. Найдите длину одной из сторон квадрата. Если вам известна только площадь (S), извлеките из ее значения квадратный корень a = √S. Далее определите периметр.
2
Дано: площадь квадрата равна 36 см². Найдите периметр фигуры.Решение 1. Найдите сторону квадрата: b = √S, b = √36 см², b =6 см. Найдите периметр: P = 4*b, P = 4*6см, P = 24 см. Или Р = 6 + 6 + 6 + 6, Р = 24см.Ответ: периметр квадрата площадью 36 см² равен 24 см.
3
Найти периметр квадрата через площадь можно, не прибегая к лишнему действию (вычислению стороны). Для этого воспользуйтесь формулой вычисления периметра, справедливой только для квадрата P = 4*√S.
4
Решение 2. Найдите периметр квадрата: P = 4*√S, P = 4*√36см², P = 24 см.Ответ: периметр квадрата равен 24 см.
5
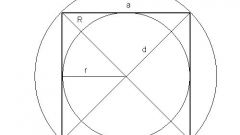
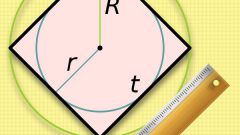
Многие параметры этой геометрической фигуры связаны между собой. Зная один из них, вы сможете найти любой другой. Существуют также следующие формулы вычисления:Диагональ: a² = 2*b², где а – диагональ, b – сторона квадрата. Или a²=2S.Радиус вписанной окружности: r = b/2, где b – сторона.Радиус описанной окружности: R = ½*d, где d – диагональ квадрата.Диаметр описанной окружности: D = f, где f – диагональ.