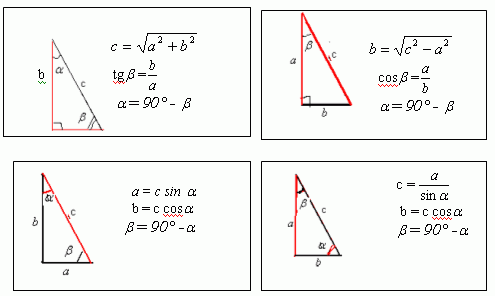Инструкция
1
Как решить задачу по геометрии, в условии которой приведены только периметр и углы? Конечно, если речь идет о остроугольном треугольнике или многоугольнике, то такую задачу без знания длины одной из сторон решить невозможно. Однако, если речь идет о прямоугольном треугольнике или прямоугольнике, то по заданному периметру можно найти его стороны. Прямоугольник имеет длину и ширину. Если провести диагональ прямоугольника, можно обнаружить, что она разбивает прямоугольник на два прямоугольных треугольника. Диагональ является гипотенузой, а длина и ширина - катетами этих треугольников. У квадрата, являющегося частным случаем прямоугольника, диагональ является гипотенузой прямоугольного равнобедренного треугольника.
2
Предположим, что имеется прямоугольный треугольник со сторонами a, b и c, у которого один из углов равен 30 , а второй 60. На рисунке видно, что a = c*sin?, а b = c*cos?. Зная, что периметр любой фигуры, в том числе и треугольника, равен сумме всех его сторон, получаем:a+b+c=c*sin ?+c*cos+c=pИз этого выражения можно найти неизвестную сторону c, которая является гипотенузой для треугольника. Так как угол ? = 30, после преобразования получим:c*sin ?+c*cos ?+c=c/2+c*sqrt(3)/2+c=pОтсюда следует, что с=2p/[3+sqrt(3)]Соответственно a = c*sin ?=p/[3+sqrt(3)],b=c*cos ?=p*sqrt(3)/[3+sqrt(3)]
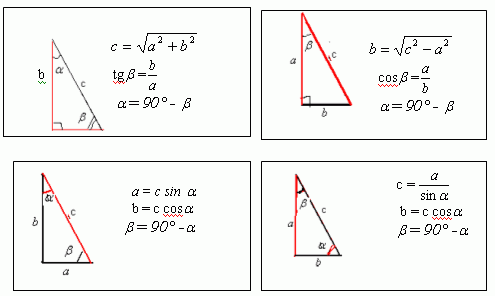
Как найти <strong>длину</strong> и <b>ширину</b> <em>периметра</em>
3
Как уже сказано выше, диагональ прямоугольника делит его на два прямоугольных треугольника с углами 30 и 60 градусов. Поскольку периметр прямоугольника равен p=2(a + b), ширину a и длину b прямоугольника можно найти, исходя из того, что диагональ является гипотенузой прямоугольных треугольников:a = p-2b/2=p[3- sqrt(3)]/2[3+sqrt (3)]
b= p-2a/2=p[1 +sqrt(3) ]/2[3+ sqrt(3)]Эти два уравнения выражены через периметр прямоугольника. По ним вычисляются длина и ширина этого прямоугольника с учетом получившихся углов при проведении его диагонали.