Инструкция
1
Если длины всех трех сторон треугольника известны (А, В и С), то для нахождения длины периметра (P) просто сложите их: P = А + В + С.
2
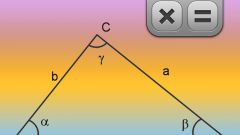
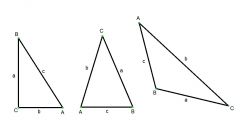
Если известны величины двух углов (α и γ) в вершинах произвольного треугольника, а также длина хотя бы одной его стороны (С), то этих данных достаточно для расчета длин недостающих сторон, а следовательно и периметра (P) треугольника. Если сторона известной длины лежит между углами α и γ, то используйте теорему синусов - длину одной из неизвестных сторон можно выразить как sin(α)∗С/(sin(180°-α-γ)), а длину другой - как sin(γ)∗С/(sin(180°-α-γ)). Для расчета периметра сложите эти формулы и добавьте к ним длину известной стороны: P = С + sin(α)∗С/(sin(180°-α-γ)) + sin(γ)∗С/(sin(180°-α-γ)).
3
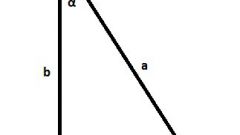
Если же сторона, длина которой известна (В), прилегает только к одному из двух известных углов (α и γ) в треугольнике, то формулы расчета длин недостающих сторон будут немного другими. Длину той из них, которая лежит напротив единственного неизвестного угла, можно определить по формуле sin(180°-α-γ)∗В/sin(γ). Для вычисления третьей стороны треугольника используйте формулу sin(α)∗В/sin(γ). Для расчета длины периметра (P) сложите обе формулы с длиной известной стороны: P = В + sin(180°-α-γ)∗В/sin(γ) + sin(α)∗В/sin(γ).
4
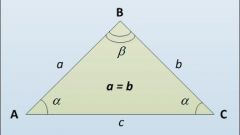
Если неизвестна длина лишь одной из сторон, а кроме длин двух других (А и В) дана величина одного из углов (γ), то используйте теорему косинусов для вычисления длины недостающей стороны - она будет равна √(А²+В²-2∗А∗В∗cos(γ)). А для нахождения длины периметра добавьте это выражение к длинам остальных сторон: P = А + В + √(А²+В²-2∗А∗В∗cos(γ)).
5
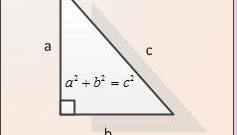
Если треугольник - прямоугольный, а недостающая сторона является его катетом, то формулу из предыдущего шага можно упростить. Для этого используйте теорему Пифагора, из которой вытекает, что длина гипотенузы равна квадратному корню из суммы квадратов известных длин катетов √(А²+В²). Добавьте к этому выражению длины катетов для вычисления периметра: P = А + В + √(А²+В²).
Видео по теме