Инструкция
1
В произвольной фигуре, ограниченной разными отрезками ломаной линии, периметр определяется последовательным измерением сторон и суммированием результатов измерения. Для правильных многоугольников нахождение периметра возможно вычислением по формулам, учитывающим связи между сторонами фигуры.
2
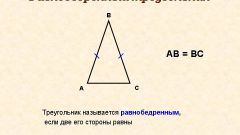
В произвольном треугольнике со сторонами а, b, с периметр Р вычисляется по формуле: Р=а+b+с. У равнобедренного треугольника две стороны равны между собой: а=b, и формула нахождения периметра упрощается до Р=2*а+с.
3
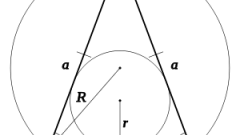
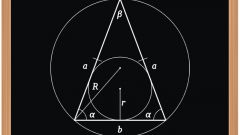
Если в равнобедренном треугольнике по условию даны размеры не всех сторон, то для нахождения периметра можно использовать другие известные параметры, например площадь треугольника, его углы, высоты, биссектрисы и медианы. Например, если известны только две равные стороны равнобедренного треугольника и любой из его углов, то третью сторону найдите по теореме синусов, из которой следует, что отношение стороны треугольника к синусу противолежащего угла есть величина постоянная для данного треугольника. Тогда неизвестная сторона может быть выражена через известную: a=b*SinА/SinВ, где А - угол против неизвестной стороны а, В - угол против известной стороны b.
4
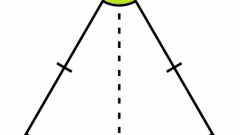
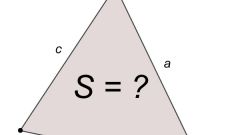
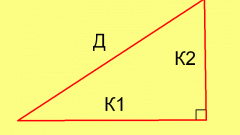
Если известна площадь S равнобедренного треугольника и его основание b, то из формулы для определения площади треугольника S=b*h/2 найдите высоту h: h=2*S/b. Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного треугольника являются гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
P=b+2*√(b²/4) +4*S²/b²).
P=b+2*√(b²/4) +4*S²/b²).