Вам понадобится
- - калькулятор;
- - таблицы синусов, косинусов и тангенсов;
- - бумага;
- - чертежные принадлежности.
Инструкция
1
Самый простой вариант задачи – когда даны все стороны трапеции. В этом случае их нужно просто сложить. Можно воспользоваться следующей формулой: p=a+b+c+d, где p – периметр, а буквами a, b, c и d обозначены стороны, противолежащие углам, обозначенным соответствующими прописными буквами.
2
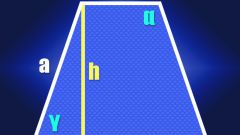
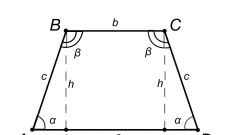
Есть дана равнобедренная трапеция, достаточно сложить два ее основания и прибавить к ним удвоенный размер стороны. То есть периметр в этом случае вычисляется по формуле: p=a+c+2b, где b – сторона трапеции, а и с – основания.
3
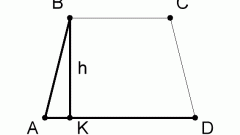
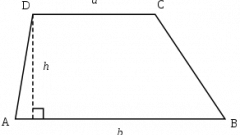
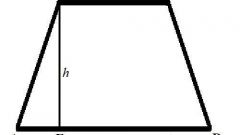
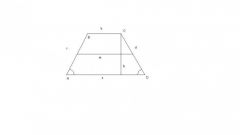
Расчеты будут несколько более длительными, если какую-то из сторон надо вычислить. Например, известно длинное основание, прилежащие к нему углы и высота. Вам нужно вычислить короткое основание и сторону. Для этого начертите трапецию ABCD, из верхнего угла B проведите высоту BE. У вас получится треугольник АВЕ. Вам известен угол А, соответственно, вы знаете его синус. В данных задачи указана также высота BE, которая одновременно является катетом прямоугольного треугольника, противолежащим известному вам углу. Чтобы найти гипотенузу АВ которая одновременно является стороной трапеции, достаточно BE разделить на sinA. Точно так же найдите длину второй стороны. Для этого нужно провести высоту из другого верхнего угла, то есть CF.
Теперь вам известны большее основание и стороны. Для вычисления периметра этого мало, нужен еще размер меньшего основания. Соответственно, в двух образовавшихся внутри трапеции треугольниках надо найти размеры отрезков AE и DF. Это можно сделать, например, через косинусы известных вам углов А и D. Косинус – это отношение прилежащего катета к гипотенузе. Чтобы найти катет, нужно гипотенузу умножить на косинус. Дальше периметр вычислите по той же формуле, что и в первом шаге, то есть сложив все стороны.
Теперь вам известны большее основание и стороны. Для вычисления периметра этого мало, нужен еще размер меньшего основания. Соответственно, в двух образовавшихся внутри трапеции треугольниках надо найти размеры отрезков AE и DF. Это можно сделать, например, через косинусы известных вам углов А и D. Косинус – это отношение прилежащего катета к гипотенузе. Чтобы найти катет, нужно гипотенузу умножить на косинус. Дальше периметр вычислите по той же формуле, что и в первом шаге, то есть сложив все стороны.
4
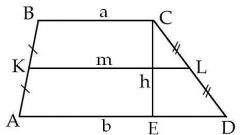
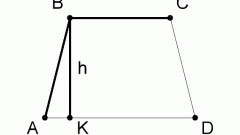
Еще один вариант: даны два основания, высота и одна из сторон, нужно найти вторую сторону. Это также лучше делать с использованием тригонометрических функций. Для этого начертите трапецию. Допустим, вам известны основания АD и ВС, а также сторона АВ и высота BF. По этим данным вы можете найти угол A (через синус, то есть отношение высоты к известной стороне), отрезок АF (через косинус или тангенс, поскольку угол вам уже известен. Вспомните также свойства углов трапеции – сумма углов, прилежащих к одной стороне, составляет 180°.
Проведите высоту CF. У вас получился еще один прямоугольный треугольник, в котором вам нужно найти гипотенузу CD и катет DF. Начните с катета. Вычтите из длины нижнего основания длину верхнего, а из полученного результата – длину уже известного вам отрезка АF. Теперь в прямоугольном треугольнике СFD вам известны два катета, то есть вы можете найти тангенс угла D, а по нему – и сам угол. После этого останется через синус этого же угла вычислить сторону CD, как уже было описано выше.
Проведите высоту CF. У вас получился еще один прямоугольный треугольник, в котором вам нужно найти гипотенузу CD и катет DF. Начните с катета. Вычтите из длины нижнего основания длину верхнего, а из полученного результата – длину уже известного вам отрезка АF. Теперь в прямоугольном треугольнике СFD вам известны два катета, то есть вы можете найти тангенс угла D, а по нему – и сам угол. После этого останется через синус этого же угла вычислить сторону CD, как уже было описано выше.
Видео по теме