Как найти углы равнобедренной трапеции

Трапеция - это плоская четырехугольная геометрическая фигура, отличительной особенностью которой является обязательная параллельность одной пары несоприкасающихся сторон. Эти стороны называются ее основаниями, а две непараллельные составляющие - боковыми сторонами. Разновидность трапеции, у которой длины боковых сторон одинаковы, называется равнобокой или равнобедренной. Формулы нахождения углов такой трапеции легко вывести из свойств прямоугольного треугольника.

Инструкция

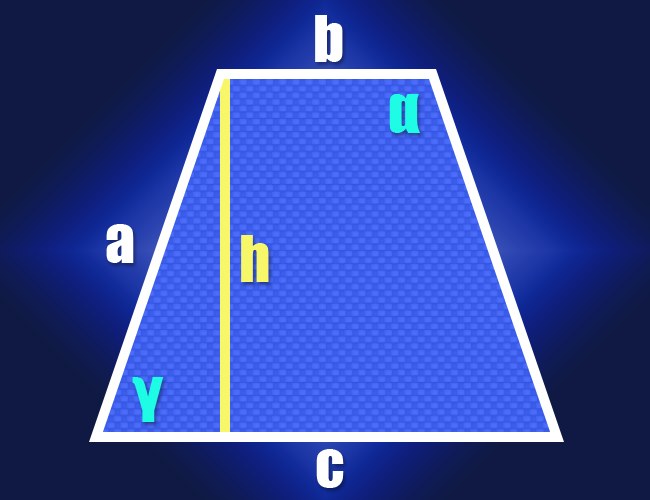
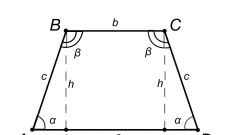
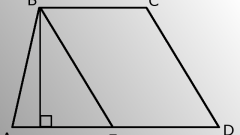
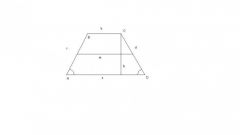
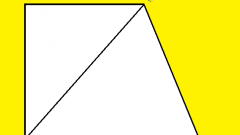
1. Если известны длины обоих оснований (b и c) и одинаковых по определению боковых сторон (a) равнобедренной трапеции, то для вычисления величины одного из ее острых углов (γ) можно использовать свойства прямоугольного треугольника. Для этого опустите высоту из любого прилегающего к короткому основанию угла. Прямоугольный треугольник будет образован высотой (катет), боковой стороной (гипотенуза) и отрезком длинного основания между высотой и ближней боковой стороной (второй катет). Длину этого отрезка можно найти, отняв от длины большего основания длину меньшего и поделив результат пополам: (c-b)/2.
2. Получив значения длин двух смежных сторон прямоугольного треугольника, переходите к вычислению угла между ними. Отношение длины гипотенузы (a) к длине катета ((c-b)/2) дает значение косинуса этого угла (cos(γ)), а функция арккосинус поможет преобразовать его в величину угла в градусах: γ=arccos(2*a/(c-b)). Так вы получите величину одного из острых углов трапеции, а поскольку она равнобедренна, то и второй острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, а это значит, что сумма двух тупых углов будет равна разности между этим числом и удвоенной величиной острого угла. Поскольку оба тупых угла тоже будут одинаковы, то для нахождения величины каждого из них (α) эту разность надо поделить пополам: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Теперь у вас есть формулы вычисления всех углов равнобедренной трапеции по известным длинам ее сторон.
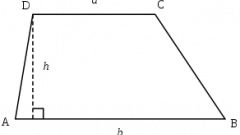
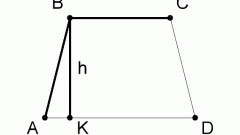
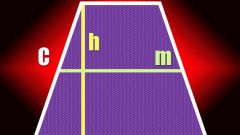
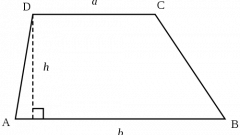
3. Если длины боковых сторон фигуры неизвестны, но дана ее высота (h), то действовать нужно по такой же схеме. В этом случае в прямоугольном треугольнике, составленном из высоты, боковой стороны и короткого отрезка длинного основания, вам будут известны длины двух катетов. Их соотношение определяет тангенс нужного вам угла, а эта тригонометрическая функция тоже имеет своего антипода, преобразующего значение тангенса в величину угла - арктангенс. Полученные в предыдущем шаге формулы острого и тупого углов трансформируйте соответствующим образом: γ=arctg(2*h/(c-b)) и α = 180°-arctg(2*h/(c-b)).