Вам понадобится
  • - боковые стороны (AB и CD);
  • - нижнее основание (AD);
  • - угол A (BAD).
Инструкция
1
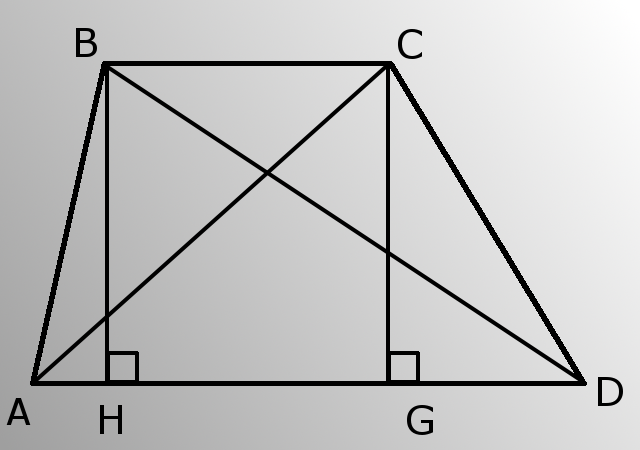
Параллельные стороны трапеции называются ее основаниями, а две другие – боковыми сторонами. Расстояние между основаниями - высота. Кроме того, вам понадобится определение прямоугольного треугольника - треугольник, у которого один из углов прямой, то есть равен 90 градусов.
2
Проведите высоту BH. Найдите ее длину из треугольника ABH. Треугольник прямоугольный, значит катет (BH), противолежащий углу A (BAD), равен произведению гипотенузы (AB) на синус угла А. BH=AB*sinA.
3
Теперь вычислите AH по теореме Пифагора из прямоугольного треугольника ABH. То есть, квадрат гипотенузы (AB) равен сумме квадратов катетов (BH и AH). AH = корень(AB*AB-HB*HB).
4
Далее рассмотрите треугольник BDH. Узнайте сторону HD. HD=AD-AH.
5
Выведите из прямоугольного треугольника BDH гипотенузу BD по той же теореме Пифагора. BD = корень(BH*BH+HD*HD). Таким образом, вам известна одна из диагоналей.
6
Проведите высоту CG. Поскольку основания трапеции параллельны, высоты BH и CG равны.
7
По теореме Пифагора из прямоугольного треугольника CGD узнайте катет GD. GD = корень(CD*CD-CG*CG).
8
Теперь для треугольника ACG найдите AG. AG=AD-GD.
9
По теореме Пифагора вычислите из прямоугольного треугольника ACG диагональ AC. AC = корень(AG*AG+CG*CG). Задача решена, вам известны обе диагонали.