Вам понадобится
- - калькулятор.
Инструкция
1
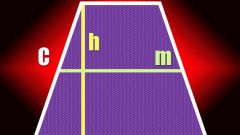
Если известны две длины - большого основания трапеции и средней линии - используйте для расчета наименьшего основания свойство трапеции. Согласно нему, средняя линия трапеции тождественна полусумме оснований. В этом случае наименьшее основание будет равно разности удвоенной длины средней линии и длины большого основания данной фигуры.
2
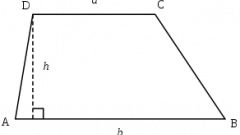
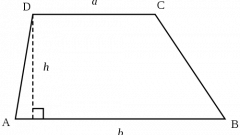
Если известны такие параметры трапеции, как площадь, высота, длина большого основания, то расчет наименьшего основания данной фигуры ведите на основе формулы площади трапеции. В этом случае конечный результат получите путем вычитания из разности частного удвоенной площади и высоты такого параметра, как длина большого основания трапеции.
3
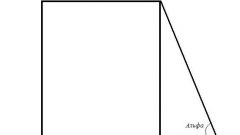
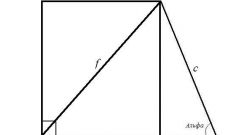
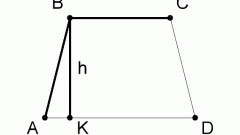
Длину наименьшей боковой стороны в прямоугольной трапеции высчитывайте по другой методике. Этот параметр будет равен произведению длины второй боковой стороны и синуса острого угла, прилежащего к ней. В тех же случаях, когда величина угла неизвестна, наименьшую боковую сторону приравнивайте к высоте трапеции и высчитывайте по теореме Пифагора. Наименьшую боковую сторону в прямоугольной трапеции находите с помощью теоремы косинусов: с²=a²+b²-2ab*cosα; где а, b, с представляют собой стороны треугольника; α является углом между сторонами а и b.
Видео по теме
Обратите внимание
Чтобы не ошибиться в вычислениях, значения синусов и косинусов берите из тригонометрических таблиц.
Полезный совет
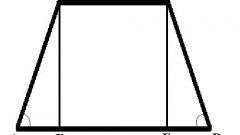
Если трапеция является остроугольной фигурой, то ее наименьшее основание высчитывайте путем вычитания из разности длины большого основания такой величины, как произведение высоты на сумму котангенсов углов при большом основании.
Для тупоугольной фигуры малое основание высчитывайте путем вычитания из разности длины большого основания такой величины, как произведение высоты на сумму разность котангенсов острого и тупого углов при большом основании.
Для тупоугольной фигуры малое основание высчитывайте путем вычитания из разности длины большого основания такой величины, как произведение высоты на сумму разность котангенсов острого и тупого углов при большом основании.
Источники:
- Трапеция (задачи про основания)