Инструкция
1
Периметр прямоугольной трапеции равен сумме длин сторон двух оснований и двух боковых сторон. Задача 1. Найдите периметр прямоугольной трапеции, если известны длины всех его сторон. Для этого сложите все четыре значения: P (периметр) = a + b + c + d.Это самый простой вариант нахождения периметра, задачи с другими начальными данными, в конечном итоге, сводятся к ней. Рассмотрим варианты.
2
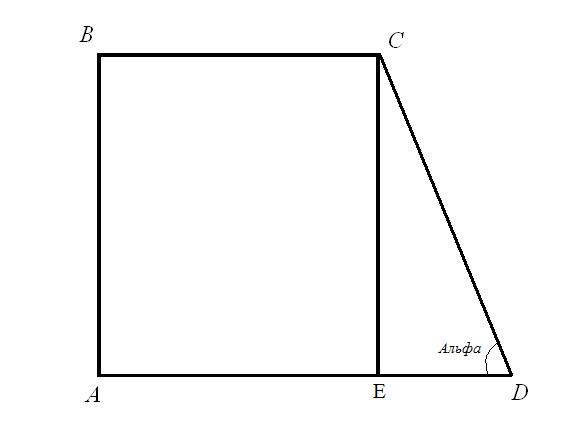
Задача 2.Найдите периметр прямоугольной трапеции, если известно нижнее основание AD = a, не перпендикулярная ему боковая сторона CD = d, а угол при этой боковой стороне ADC равен Альфа.Решение.Проведите высоту трапеции из вершины C на большее основание, получим отрезок CE, трапеция разделилась на две фигуры - прямоугольник ABCE и прямоугольный треугольник ECD. Гипотенуза треугольника - это известная нам боковая сторона трапеции CD, один из катетов равен перпендикулярной боковой стороне трапеции (по правилу прямоугольника две параллельные стороны равны - AB = CE), а другой - отрезок, длина которого равна разности оснований трапеции ED = AD - BC.
3
Найдите катеты треугольника: по существующим формулам CE = CD*sin(ADC) и ED = CD*cos(ADC).Теперь вычислите верхнее основание - BC = AD - ED = a - CD*cos(ADC) = a - d*cos(Альфа).Узнайте длину перпендикулярной боковой стороны - AB = CE = d*sin(Альфа).Итак, вы получили длины всех сторон прямоугольной трапеции.
4
Сложите полученные значения, это и будет периметр прямоугольной трапеции:P = AB + BC + CD + AD = d*sin(Альфа) + (a - d*cos(Альфа)) + d + a = 2*a + d*(sin(Альфа) - cos(Альфа) + 1).
5
Задача 3.Найдите периметр прямоугольной трапеции, если известны длины его оснований AD = a, BC = c, длина перпендикулярной боковой стороны AB = b и острый угол при другой боковой стороне ADC = Альфа.Решение.Проведите перпендикуляр CE, получите прямоугольник ABCE и треугольник CED.Теперь найдите длину гипотенузы треугольника CD = AB/sin(ADC) = b/sin(Альфа).Итак, вы получили длины всех сторон.
6
Сложите полученные значения:P = AB + BC + CD + AD = b + c + b/sin(Альфа) + a = a + b*(1+1/sin(Альфа) + с.