Инструкция
1
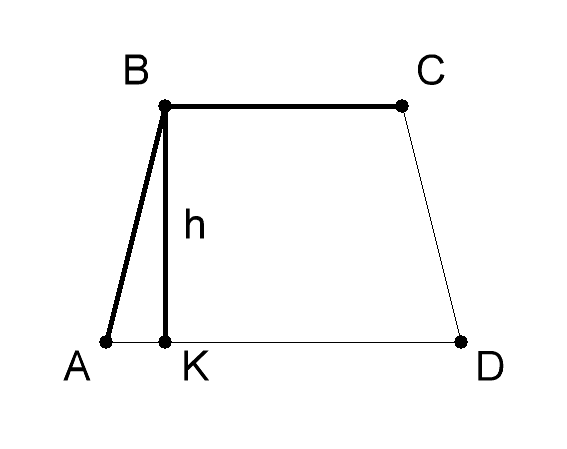
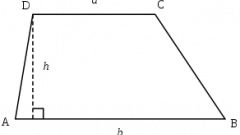
Измерьте основания и высоту трапеции АВСД. Обычно их величина дается в условиях задачи. Пусть в данном примере решения задачи основание АD (а) трапеции будет равно 10 см, основание BC (b) - 6 см, высота трапеции BK (h) - 8 см. Примените геометрическую формулу для нахождения площади трапеции, если известны длины её оснований и высоты - S= 1/2 (a+b)*h, где: - a - величина основания AD трапеции ABCD,- b - величина основания BC,- h - величина высоты BK.
2
Найдите сумму длин оснований трапеции: АD + BC (10 см + 6 см = 16 см). Поделите полученную сумму на 2 (16/2=8 см). Умножьте полученное число на длину высоты ВС трапеции ABCD (8*8 = 64). Итак, площадь трапеции ABCD с основаниями, равными 10 и 6 см, и высотой, равной 8 см, будет равна 64 кв.см.
3
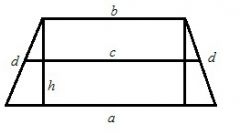
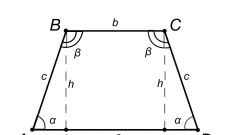
Измерьте основания и боковые стороны трапеции АВСД. Пусть в данном примере решения задачи основание АD (a) трапеции будет равно 10 см, основание BC (b) - 6 см, сторона AB (c) - 9 см и сторона CD (d)- 8 см. Примените формулу для нахождения площади трапеции, если известны её основания и боковые стороны - S=(a+b)/2*(√ с2 - ((b-a)2+c2-d2/(2(b-a))2, где:- a - величина основания AD трапеции ABCD,- b - величина основания BC,- с - величина боковой стороны AB,- d - величина боковой стороны CD.
4
Подставьте длины оснований трапеции в формулу: S=(a+b)/2*(√ с2 - ((b-a)2+c2-d2/(2(b-a))2. Решите следующее выражение: (10+6)/2*√(9*9-((10-6)2+(9*9-8*8)/(2*(10-6))2. Для этого упростите выражение, сделав вычисления в скобках: 8*√ 81-((16+81-64)/8)2= 8*√(81-17). Найдите значение произведения: 8*√(81-17)=8*8=64. Итак, площадь трапеции ABCD с основаниями, равными 10 и 6 см, и боковыми сторонами, равными 8 и 9 см будет равна 64 кв.см.
Обратите внимание
Если две боковые стороны трапеции равны, то она называется равнобедренной. Её диагонали равны между собой, равны также углы при основании.
Источники:
- Формулы он-лайн