Инструкция
1
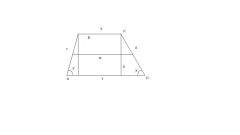
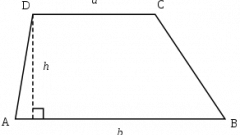
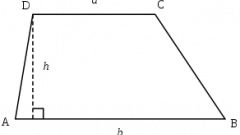
В решении большинства задач по определению углов четырехугольной трапеции учитываются те или иные свойства фигуры. При этом результаты задач могут быть различны из-за вариативных исходных данных. Если перед началом решения даны условия, что известны только два угла, относящиеся к основанию трапеции, решение задачи сводится к следующим действиям:Определите буквенные значения для трапеции – MNOP, а известные углы назовите соответственно ∠NMP и ∠OMP. Значения для этих углов будут равняться: ∠NMP = a и ∠OMP = b. Вам необходимо вычислить углы при верхнем основании ∠MNO и ∠NOP.
2
Воспользуйтесь свойством трапеции, когда сумма обоих углов при боковой стороне равняется 180°. В этом случае искомые углы: ∠MNO = (180° – a), а ∠NOP = (180° – b).
3
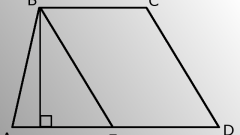
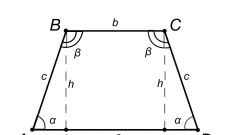
При других исходных данных – равенства определенных сторон трапеции и известном значении одного из углов – набор действий по решению задачи может принять следующий вид. Используйте те же обозначения для трапеции MNOP, только в данном случае задайте, что ее стороны MN и OP, а также верхнее основание NO равны по длине между собой. Проведенная же диагональ MO составляет с основанием MP угол ∠OMP = с.
4
Учитывая, что в треугольнике MNO две его стороны равняются друг другу, он является равнобедренным и углы ∠NMO = ∠NOM = d, а угол ∠MNO = e. Поскольку сумма всех углов в треугольнике равняется 180°, следовательно (2d + e) = 180°. В результате e = (180° – 2d).
5
Используя свойство трапеции о сумме углов, прилегающих к одной стороне, равной 180°, определите другую формулу (e + d + c) = 180°. Тогда при e = (180° – 2d) формула приобретает вид (180° – 2d + d + c) = 180° или c = d.
6
В результате вы найдете углы ∠NMO = d = c и ∠MNO = e = 180° – 2c. Поскольку заданная трапеция является равнобедренной, то согласно ее свойству равнобокости диагонали ее равны и соответственно равны углы при обоих основаниях. Значит ∠OPM = ∠NOP = 180° – 2c.
Видео по теме