Как найти углы четырёхугольника

Для решения этой задачи методами векторной алгебры, вам необходимо знать следующие понятия: геометрическая векторная сумма и скалярное произведение векторов, а также следует помнить свойство суммы внутренних углов четырехугольника.

Вам понадобится

• - бумага;
• - ручка;
• - линейка.

Инструкция

1. Вектор – это направленный отрезок, то есть величина, считающаяся заданной полностью, если задана его длина и направление (угол) к заданной оси. Положение вектора больше ничем не ограничено. Равными считаются два вектора, обладающие одинаковыми длинами и одним направлением. Поэтому при использовании координат векторы изображают радиус-векторами точек его конца (начало располагается в начале координат).
2. По определению: результирующим вектором геометрической суммы векторов называется вектор, исходящий из начала первого и имеющего конец в конце второго, при условии, что конец первого, совмещен с началом второго. Это можно продолжать и далее, строя цепочку аналогично расположенных векторов.
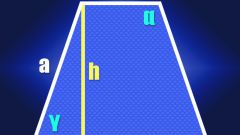
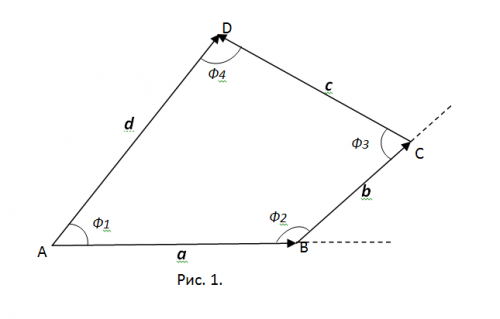
   Изобразите заданный четырехугольник ABCD векторами a, b, c и d в соответствии рис. 1. Очевидно, что при таком расположении результирующий вектор d=a+ b+c.
   
3. Скалярное произведение в данном случае удобнее всего определить на основе векторов a и d. Скалярное произведение, обозначаемое (a, d)= |a||d|cosф1. Здесь ф1 – угол между векторами a и d.
   Скалярное произведение векторов, заданных координатами, определяется следующими выражением:
   (a(ax, ay), d(dx, dy))=axdx+aydy, |a|^2= ax^2+ ay^2, |d|^2= dx^2+ dy^2, тогда
   cos Ф1=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)).
4. Основные понятия векторной алгебры в привязке к поставленной задаче, приводят к тому, что для однозначной постановки этой задачи достаточно задание трех векторов, расположенных, допустим, на AB, BC, и CD, то есть a, b, c. Можно конечно сразу задать координаты точек A, B, C, D, но этот способ является избыточным (4 параметра вместо 3-х).
5. Пример. Четырехугольник ABCD задан векторами его сторон AB, BC, CD a(1,0), b(1,1), c(-1,2). Найти углы между его сторонами.
   Решение. В связи с изложенным выше, 4-й вектор (для AD)
   d(dx,dy)=a+ b+c={ax+bx +cx, ay+by+cy}={1,3}. Следуя методике вычисления угла между векторами а
   cosф1=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2))=1/sqrt(10), ф1=arcos(1/sqrt(10)).
   -cosф2=(axbx+ayby)/(sqrt(ax^2+ ay^2)sqrt(bx^2+ by^2))=1/sqrt2, ф2=arcos(-1/sqrt2), ф2=3п/4.
   -cosф3=(bxcx+bycy)/(sqrt(bx^2+ by^2)sqrt(cx^2+ cy^2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1.
   В соответствии с замечанием 2 - ф4=2п- ф1 - ф2- ф3=п/4.