Вам понадобится
- - таблица синусов;
- - таблица косинусов;
- - таблица тангенсов.
Инструкция
1
В условиях задачи может быть указан меньший угол. Вспомните, чему равна сумма углов, прилежащих к одной стороне. Она у любого ромба составляет 180°. То есть вам достаточно из 180° вычесть размер известного угла. Начертите ромб. Обозначьте больший угол как α, а меньший – как β. Формула в этом случае будет выглядеть как α=180°-β.
2
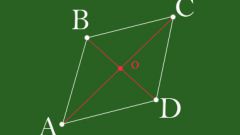
В задаче могут быть указаны также размер стороны и длина одной из диагоналей. В этом случае нужно вспомнить свойства диагоналей ромба. В точке пересечения они делятся пополам. Диагонали перпендикулярны друг другу, то есть при решении задачи можно будет использовать свойства прямоугольных треугольников. Еще одна важная деталь каждая из диагоналей одновременно является и биссектрисой угла.
3
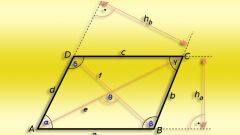
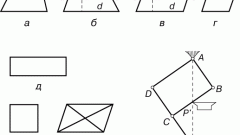
Для наглядности сделайте чертеж. Начертите ромб ABCD. Проведите в нем диагонали d1 и d2. Допустим, известная вам диагональ d1 соединяет меньшие углы. Обозначьте точку их пересечения как О, большие углы ABC и CDA– как α, а меньшие – как β. Каждый из углов делится диагональю пополам. Рассмотрите прямоугольный треугольник АОВ. Вам известны стороны АВ и ОА, равная половине диагонали d1. Они представляют собой гипотенузу и катет противолежащего угла.
4
Вычислите синус угла АВО. Он равен отношению катета ОА к гипотенузе АВ, то есть sinАВО= ОА/АВ. По таблице синусов найдите размер угла. Вспомните, что он равен половине большего угла ромба. Соответственно, для определения искомого полученный размер умножьте на 2.
5
Если в условиях дан размер диагонали d2, соединяющей большие углы, способ решения будет аналогичен предыдущему, только вместо синуса используется косинус – отношение прилежащего катета к гипотенузе.
6
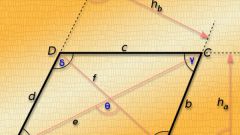
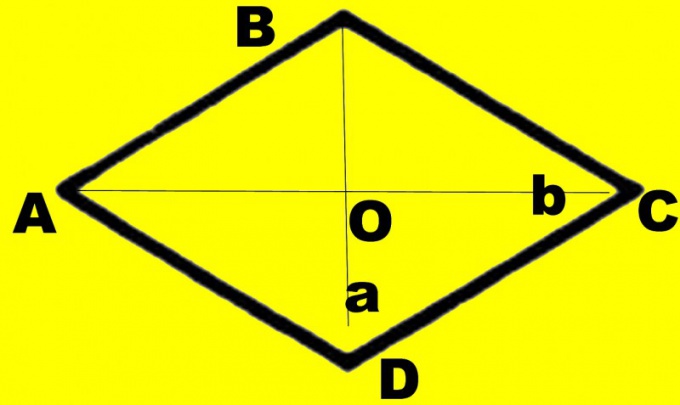
В условиях могут быть заданы только размеры диагоналей. В этом случае тоже понадобится чертеж, но, в отличие от предыдущих задач, он может быть точным. Проведите диагональ d1. Разделите ее пополам. К точке пересечения проведите диагональ d2 так, чтобы она тоже делилась на две равные части. Концы отрезков соедините по периметру. Обозначьте ромб как ABCD, точку пересечения диагоналей – как О.
7
Сторону ромба в данном случае вам вычислять не нужно. У вас образовался прямоугольный треугольник АОВ, у которого вам известны два катета. Отношение противолежащего катета к прилежащему называется тангенсом. Чтобы найти tgАВО, разделите ОА на ОВ. Найдите в таблице тангенсов нужное значение угла, а затем умножьте его на два.
8
Некоторые компьютерные программы позволяют не только вычислить больший угол ромба по заданным параметрам, но и сразу же начертить эту геометрическую фигуру. Это можно сделать, например, в программе AutoCAD. В этом случае таблицы синусов и тангенсов, конечно же, не нужны.