Инструкция
1
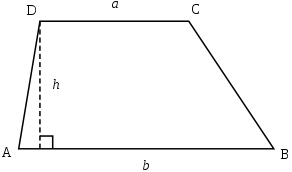
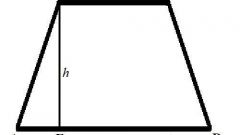
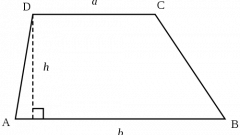
Допустим, в трапеции известны длины параллельных сторон (a и b, соответственно), а также и длина ее высоты h, то рассчитать площадь трапеции можно, применив следующую формулу:
S = ((a+b)*h)/2
Пример: длина основания и противоположной ей стороны трапеции равна 28 и 22 см соответственно. Высота данной трапеции 30 см
Для того, чтобы найти площадь данной фигуры, надо воспользоваться формулой, указанной выше:
S = ((28+22)*30)/2 = 750 см²
S = ((a+b)*h)/2
Пример: длина основания и противоположной ей стороны трапеции равна 28 и 22 см соответственно. Высота данной трапеции 30 см
Для того, чтобы найти площадь данной фигуры, надо воспользоваться формулой, указанной выше:
S = ((28+22)*30)/2 = 750 см²
2
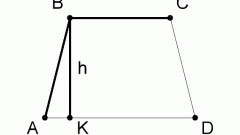
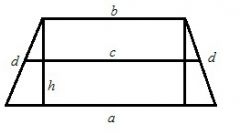
Когда у трапеции известны длина ее средней линии m и ее высота h, то найти площадь трапеции становится еще проще, зная эту формулу:
S = m*h
Пример: длина средней линии трапеции 15 см, высота ее 10 см
Применяя указанную выше формулу, получается:
S = 15*10 = 150 см²
S = m*h
Пример: длина средней линии трапеции 15 см, высота ее 10 см
Применяя указанную выше формулу, получается:
S = 15*10 = 150 см²
3
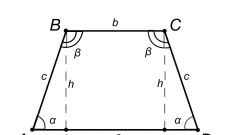
Допустим, дана равнобедренная трапеция, вокруг которой описана окружность, радиус которой равен r, а угол при основании трапеции равен α. В таком случае, площадь рассчитывается таким способом:
S = (4*r²)/sinα
Пример: вокруг равнобедренной трапеции описана окружность радиусом 20 см, угол при основании данной трапеции равен 45°. Тогда площадь находится так:
S = (4*15²)/sin45°
S = 1273 см²
S = (4*r²)/sinα
Пример: вокруг равнобедренной трапеции описана окружность радиусом 20 см, угол при основании данной трапеции равен 45°. Тогда площадь находится так:
S = (4*15²)/sin45°
S = 1273 см²
Обратите внимание
Равнобедренная трапеция обладает рядом свойств:
если через середины оснований провести прямую, она будет делить трапецию на два равных прямоугольника, являясь ко всему еще и осью ее симметрии;
углы, находящиеся при основании трапеции, равны;
Вокруг подобной трапеции можно описать окружность;
Внутрь равнобедренной трапеции можно еще и вписать окружность.
Стоит отметить, что если трапеция является прямоугольной, то одна из сторон, прилегающих к прямому углу, является, ко всему еще, и высотой данной трапеции.
Помимо всего прочего, трапеция является частным случаем другого четырехугольника - параллелограмма, ведь у обоих фигур есть пара параллельных между собой сторон
если через середины оснований провести прямую, она будет делить трапецию на два равных прямоугольника, являясь ко всему еще и осью ее симметрии;
углы, находящиеся при основании трапеции, равны;
Вокруг подобной трапеции можно описать окружность;
Внутрь равнобедренной трапеции можно еще и вписать окружность.
Стоит отметить, что если трапеция является прямоугольной, то одна из сторон, прилегающих к прямому углу, является, ко всему еще, и высотой данной трапеции.
Помимо всего прочего, трапеция является частным случаем другого четырехугольника - параллелограмма, ведь у обоих фигур есть пара параллельных между собой сторон
Источники:
- как находится площадь трапеции