Инструкция
1
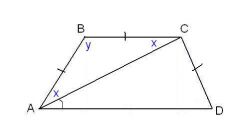
Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).
2
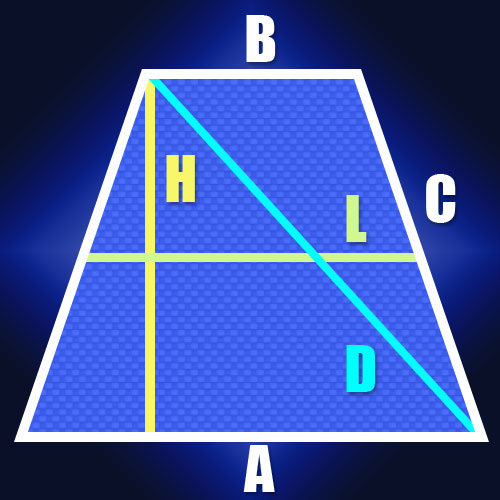
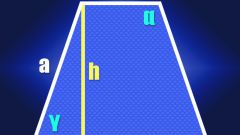
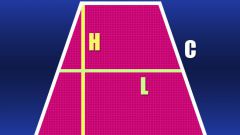
Если длины сторон не известны, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) тоже вычислить несложно. Так как длина средней линии равна полусумме оснований трапеции, то это дает возможность найти длину отрезка между точкой на большем основании, в которую опущена высота, и вершиной, прилегающей к этому основанию. В равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Так как диагональ замыкает этот отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Например, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L² + H²).
3
Если известны длины обоих оснований равнобедренной трапеции (A и B) и ее высота (H), то, как и в предыдущем случае, можно вычислить длину отрезка между точкой, опущенной на большую сторону высоты и прилегающей к ней вершиной. Формула из предыдущего шага трансформируется к такому виду: D=√((A + B)²/4 + H²).
Источники:
- диагональ в равнобедренной трапеции



Утверждение не верное: диагонали равнобедренной трапеции не являются гипотенузой треугольника с катетами 1 боковая сторона 2 основание трапецииНо утверждение о том, что сумма квадратов диагоналей равна сумме квадратов всех сторон- верное)))
1
Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей. Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²)."
Это утверждение является неверным!!!! Не вводите в заблуждение!!! Откуда Вы взяли, что:"сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей"???
Утверждение не верное: диагонали равнобедренной трапеции не являются гипотенузой треугольника с катетами 1 боковая сторона 2 основание трапецииНо утверждение о том, что сумма квадратов диагоналей равна сумме квадратов всех сторон- верное)))
НЕВЕРНОЕ, так как
сумма квадратов диагоналей ПАРАЛЛЕЛОГРАММА равна сумме квадратов всех его сторон!!
А ПАРАЛЛЕЛОГРАММ НЕ ЕСТЬ ТРАПЕЦИЯ!