Как найти основание трапеции, если известны диагонали

Следует сразу сделать оговорку, что трапецию при таких условиях восстановить не удастся. Их бесконечно много, так как для точного описания фигуры на плоскости необходимо задание не менее трех числовых параметров.

Инструкция

1. Поставленную задачу и основные позиции ее решения демонстрирует рис. 1.Предположим, что рассматриваемая трапеция – это AВCD. В ней даны длины диагоналей AC и BD. Пусть они задаются векторами p и q. Значит длины этих векторов (модули), |p| и |q|, соответственно.
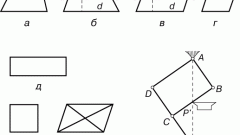
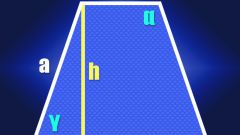
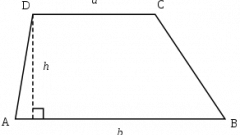
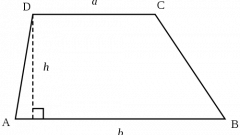
2. Чтобы упростить решение поставленной задачи, точку А следует поместить в начало координат, а точку D – на оси абсцисс. Тогда эти точки будут иметь следующие координаты: A(0, 0), D(xd, 0). Фактически число xd совпадает с искомой длиной основания AD. Пусть |p|=10 и |q|=9. Так как в соответствии с построением вектор p лежит на прямой АС, то координаты этого вектора равны координатам точки С. Методом подбора можно определить, что точка С с координатами (8, 6), удовлетворяет условию задачи. В силу параллельности AD и ВС, точка В задается координатами (xb, 6).
3. Вектор q лежит на диагонали BD. Поэтому его координаты q={xd-xb, yd-yb}=={xd-xb, -6}.|q|^2=81 и |q|^2=(xd-xb)^2 +36=81. (xd-xb)^2=45, xd=3sqrt(5)+xb. Как уже было сказано в начале, исходных данных не хватает. В том решении, которое предложено сейчас xd зависит от xb, то есть, по крайней мере, следует задать xb. Пусть xb=2. Тогда xd=3sqrt(5)-2=4,7. Это и есть длина нижнего основания трапеции (по построению).