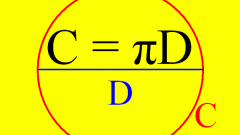Инструкция
1
Для измерения периметра круга на местности используйте специальное устройство - курвиметр. Чтобы узнать с его помощью длину окружности, агрегат нужно просто прокатить по ней колесом. Такие же приборы, но гораздо меньших размеров, используются и для определения длины любых кривых линий, включая окружности, на чертежах и картах.
2
Если нужно вычислить длину окружности (L) по известному диаметру (d), умножьте его на число Пи (3,1415926535897932384626433832795…), округлив количество знаков до нужной степени точности: L=d*π. Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*π.
3
Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*√(S*π).
4
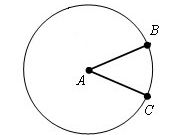
Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (θ), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять θ/360 от общей площади круга, которую можно выразить формулой s*360/θ. Подставьте ее в приведенное выше равенство: L = 2*√((s*360/θ)*π) = 2*√(s*360*π/θ). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять θ/(2*π) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*√((s*2*π/θ)*π) = 2*√(s*2*π²/θ) = 2*π*√(2*s/θ).
5
Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (θ) - в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/θ, а если он дан в радианах, формула должна быть такой: L = l*2*π/θ.
Видео по теме