Инструкция
1
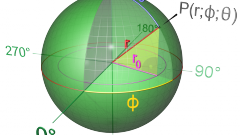
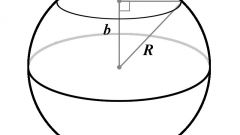
Кругом радиуса R является такое геометрическое место точек плоскости, что расстояние от центра круга до них не превышает радиуса. Граница круга – окружность – геометрическое место точек, расстояние от которых до центра равно радиусу R.
2
Площадь – характеристика плоской фигуры. Условно можно сказать, что она показывает, сколько места занимает фигура на плоскости. В общем случае, площадь находится путем взятия определенного интеграла от функции y(x).
3
Если известен радиус круга, найдите его площадь по формуле S=π•R², где S – площадь, π – число «пи», R – радиус. Число «пи» – трансцендентное иррациональное число, константа, равная примерно 3,14. Она выражает отношение длины окружности к длине диаметра: π=L/D=L/2R.
4
Пример. Окружность имеет радиус 2 см. Вычислите площадь круга, ограниченного этой окружностью.Решение. Если применить формулу для нахождения площади круга через радиус, то S=π•R²=π•2²=4π≈3,14•2²≈12,56 (см²). Иногда число π не подставляют, оставляя ответ в виде S=4π. Такой ответ менее наглядный (трудно представить число «пи»), но математически более точный.
5
Если уже известна длина окружности, можно считать площадь круга через нее: S=L•R/2. Кстати, длина окружности выражается через радиус формулой L=2•π •R.
6
Построив в круге центральный угол, можно получить сектор. Сектором называют часть круга, ограниченную дугой и двумя радиусами, которые соединяют центр круга с концами этой дуги. Чтобы найти площадь сектора, надо знать не только радиус, но и угол α: S(сектора)=α•R²/2. Здесь α – угол в радианах. Длина дуги определяется соотношением L(дуги)=α•R.
7
В комплексном анализе существует такое идиоматическое понятие, как единичный круг – круг радиуса 1. Его площадь, соответственно, равна S=π.
Видео по теме