Инструкция
1
Параллепипед – это призма, в основании которой лежит параллелограмм. Параллелограммом называется четырехугольник, противолежащие стороны которого равны и параллельны. Параллелепипед имеет шесть граней – верхнее и нижнее основание и 4 боковых грани. Все они являются параллелограммами. Поскольку в условии не указывается угол наклона боковых граней к основанию, можно считать, что призма является прямой. Отсюда следует уточнение: у прямой призмы боковые грани – прямоугольники.
2
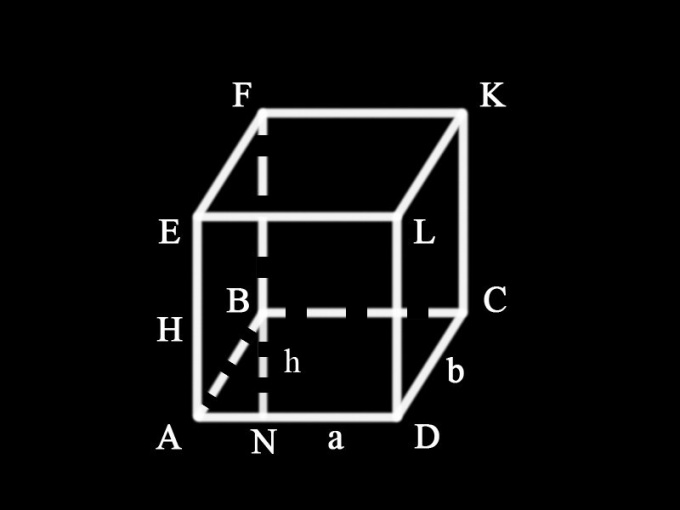
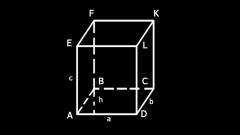
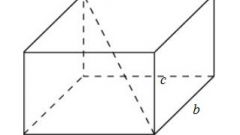
Для того чтобы найти площадь поверхности параллелепипеда, нужно найти площадь его оснований и площадь боковой поверхности. Для этого необходимо знать длину сторон основания параллелепипеда и длину его ребра. Для определения площади основания нужно провести высоту параллелограмма. Можно считать, что эти величины известны, поскольку в условии этот пункт не оговаривается. Для удобства вводятся обозначения:AD = BC = a – основания параллелограмма;AB = CD = b – боковые стороны параллелограмма;BN = h – высота параллелограмма;AE = DL = CK = BF = H – ребро параллелепипеда.
3
Площадь параллелограмма определяется как произведение его основания на высоту, т.е. ah. Поскольку верхнее и нижнее основания равны, их общая площадь S = 2ah.
4
Поскольку боковые грани являются прямоугольниками, их площадь вычисляется как произведение сторон. Одна сторона грани AELD является ребром параллелепипеда и равняется H, а другая стороной его основания и равняется a. Площадь грани: aH. Боковые грани параллелепипеда попарно равны и параллельны. Грань AELD равна грани BFKC. Их общая площадь S = 2aH.
5
Грань AEFB равна грани DLKC. Сторона AB совпадает с боковой стороной основания параллелепипеда и равняется b, сторона AE равна H. Площадь грани AEFB равна bH. Сумма площадей этих граней S = 2bH. Боковая поверхность параллелепипеда: 2aH+2bH.
6
Таким образом, общая площадь поверхности параллелепипеда: S = 2ah+2aH+2bH или S = 2(ah+aH+bH)Задача решена.