Инструкция
1
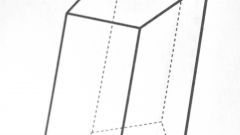
Параллелепипед – пространственная геометрическая фигура, имеющая три измерения: длину, высоту и ширину. В связи с этим он имеет две горизонтальные грани, называемые основаниями, а также четыре боковые. Все они имеют форму параллелограмма, но бывают и частные случаи, которые упрощают не только графическое изображение задачи, но и сами расчеты.
2
Основными числовыми характеристиками параллелепипеда являются площадь поверхности и объем. Различают полную и боковую поверхность фигуры, которые получаются суммированием площадей соответствующих граней, в первом случае – всех шести, во втором – только боковых.
3
Чтобы найти боковую поверхность параллелепипеда, сложите площади четырех граней. Исходя из свойства фигуры, согласно которому противолежащие грани параллельны и равны, запишите:S = 2•Sб1 + 2•Sб2.
4
Рассмотрите для начала общий случай, когда фигура наклонная: основания лежат в параллельных плоскостях, но смещены относительно друг друга:Sб1 = a•h; Sб2 = b•h, где а и b – основания каждого бокового параллелограмма, h – высота параллелепипеда.S = (2•a + 2•b)•h.
5
Посмотрите внимательно на выражение, стоящее в скобках. Величины a и b можно представить не только, как основания боковых ребер, но и как стороны основания параллелепипеда, тогда это выражение есть не что иное, как его периметр:S = P•h.
6
Наклонный параллелепипед превращается в прямой, если угол между основанием и боковым ребром становится прямым. Тогда высота параллелепипеда равна длине боковой грани:S = P•с.
7
Прямоугольный параллелепипед – популярная форма исполнения многих конструкции: домов, предметов мебели, коробок, моделей бытовой техники и пр. Это связано с простотой их возведения/создания, поскольку все углы составляют 90°. Боковая поверхность такой фигуры аналогична такой же числовой характеристике прямого, различие между ними проявляется только при расчете полной поверхности.
8
Куб – параллелепипед, у которого все измерения равны:S = 4•Sб = 4•a².
Видео по теме