Инструкция
1
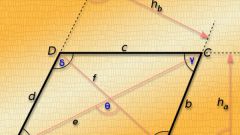
Если в условиях задачи даны длины двух смежных сторон параллелограмма (a и b) и величина угла между ними (γ), то этого будет достаточно для вычисления обоих параметров. Для расчета периметра (P) четырехугольника сложите длины сторон и вдвое увеличьте полученное значение: P = 2*(a+b). Вычислять площадь (S) фигуры придется с помощью тригонометрической функции - синуса. Перемножьте длины сторон, а результат умножьте на синус известного угла: S = a*b*sin(γ).
2
Если известна длина лишь одной из сторон (a) параллелограмма, но есть данные о высоте (h) и величине угла (α) в любой из вершин многоугольника, то это позволит найти и периметр (P) и площадь (S). Сумма всех углов в любом четырехугольнике равна 360°, а в параллелограмме те из них, что лежат в противоположных вершинах, одинаковы. Поэтому для нахождения величины оставшегося неизвестным угла отнимите от 180° величину известного. После этого рассмотрите треугольник, составленный из высоты и лежащего напротив него угла, величины которых известны, а также неизвестной пока стороны. Примените к нему теорему синусов, и выясните, что длина стороны будет равна отношению высоты к синусу угла, лежащего напротив нее: h/sin(α).
3
После проведения предварительных расчетов предыдущего шага составьте нужные формулы. Подставьте полученное выражение в формулу нахождения периметра из первого шага и получите такое равенство: P = 2*(a+h/sin(α)). В том случае, если высота соединяет две противоположные стороны параллелограмма, длина которых дана в исходных условиях, для нахождения площади просто перемножьте эти два значения: S=a*h. Если же это условие не соблюдено, то подставьте в формулу выражение для другой стороны, полученное в предыдущем шаге: S=a*h/sin(α).
Видео по теме