Инструкция
1
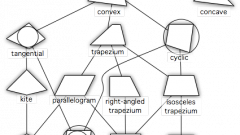
Вспомните определение параллелограмма. Это четырехугольник, противоположные стороны которого равны и параллельны. Кроме того, сумма углов, прилежащих к одной стороне, равна 180°. Этим же свойством обладает и прямоугольник, только он должен соответствовать еще одному условию. Углы, прилежащие к одной стороне, у него равны и составляют каждый 90°. То есть в любом случае вам нужно будет доказать именно то, что у заданной фигуры не только стороны параллельны и равны, но все углы являются прямыми.
2
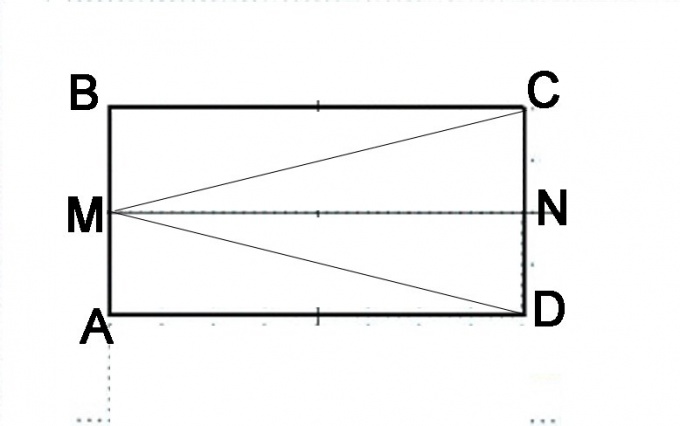
Начертите параллелограмм АВСD. Разделите сторону АВ пополам и поставьте точку М. Соедините ее с вершинами углов С и D. Вам нужно доказать, что углы МАС и МВD равны. Сумма их, согласно определению параллелограмма, составляет 180°. Для начала же вам надо доказать равенство треугольников МАС и МВD, то есть что отрезки МС и MD равны между собой.
3
Сделайте еще одно построение. Разделите сторону СD пополам и поставьте точку N. Рассмотрите внимательно, из каких геометрических фигур состоит теперь исходный параллелограмм. Он составлен из двух параллелограммов AMND и MBCN. Его можно представить и состоящим из треугольников DMB, МАС и МВD. То, что AMND и MBCN являются одинаковыми параллелепипедами, можно доказать, исходя из свойств параллелепипеда. Отрезки АМ и МВ равны, отрезки NC и ND равны тоже и представляют они собой половинки противоположных сторон параллелепипеда, которые по определению одинаковы. Соответственно, линия MN будет равна сторонам AD и ВС и параллельна им. А значит, у этих одинаковых параллелепипедов диагонали будут равны, то есть отрезок MD равен отрезку MC.
4
Сравните треугольники МАС и МВD. Вспомните признаки равенства треугольников. Их три, и в данном случае удобнее всего доказывать равенство по трем сторонам. Стороны МА и МB одинаковы, поскольку точка М находится как раз на середине отрезка AB. Стороны АD и BC равны по определению параллелограмма. Равенство сторон MD и MC вы доказали в предыдущем шаге. То есть треугольники равны, а это значит, что равны и все их элементы, то есть угол МАD равен углу МВС. Но эти углы прилежат к одной стороне, то есть сумма их составляет 180°. Разделив это число пополам, вы получите размер каждого угла - 90°. То есть все углы данного параллелограмма являются прямыми, а это значит, что он представляет собой прямоугольник.