Частный случай параллелограмма - прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника, а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.
Постройте прямоугольник EFGH. Запишите известные данные: диагональ прямоугольника EG и угол α, полученный от пересечения двух равных диагоналей FH и EG. Постройте на рисунке диагонали и отметьте между ними угол α.
2
Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями треугольник EFА. Согласно свойству прямоугольника его диагонали равны и делятся пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА является равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.
3
Далее вычислите первую сторону EF прямоугольника. Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА равна EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.
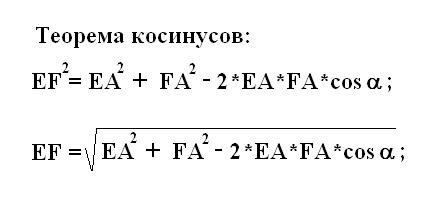
4
Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.
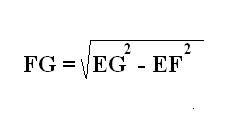
5
В соответствии со свойствами прямоугольника его противолежащие ребра равны. Таким образом сторона GH равна найденной стороне EF, а HЕ = FG. Запишите в ответ все вычисленные стороны прямоугольника.
