Вам понадобится
- Лист бумаги, линейка, карандаш, калькулятор с функцией вычисления корней.
Инструкция
1
Прямоугольник - это четырехугольник, все углы которого прямые. Диагональ прямоугольника – отрезок прямой, соединяющий две противоположные его вершины.
2
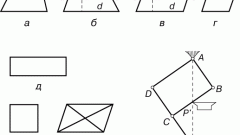
На листе бумаги с помощью линейки и карандаша нарисуйте произвольный прямоугольник АВСD. Лучше это сделать на тетрадном листе в клетку – так проще будет нарисовать прямые углы. Соедините отрезком вершины прямоугольника А и С. Полученный отрезок АС является диагональю прямоугольника АВСD.
3
4
Гипотенуза – это сторона треугольника, противолежащая прямому углу. Катеты – стороны треугольника, прилежащие к прямому углу. Применительно к треугольникам АВС и АСD: АВ и ВС, АD и DC– катеты, АС – общая гипотенуза для обоих треугольников (искомая диагональ). Следовательно, АС в квадрате = квадрат АВ + квадрат ВС или АС в квадрате = квадрат АD + квадрат DС. Подставьте значения длин сторон прямоугольника в вышеприведенную формулу и вычислите длину гипотенузы (диагонали прямоугольника).
5
Например, стороны прямоугольника АВСD равны следующим значениям: АВ = 5 см и ВС = 7см. Квадрат диагонали АС данного прямоугольника рассчитывается по теореме Пифагора: АС в квадрате = квадрат АВ + квадрат ВС = 52+72 = 25 + 49 = 74 кв.см. С помощью калькулятора вычислите значение квадратного корня 74. У вас должно получиться 8,6 см (округленное значение). Имейте в виду, что по одному из свойств прямоугольника, его диагонали равны. Значит длина второй диагонали BD прямоугольника АВСD равна длине диагонали АС. Для вышеприведенного примера эта величина составляет 8,6 см.
Видео по теме
Источники:
- как найти длину диагонали прямоугольника