Инструкция
1
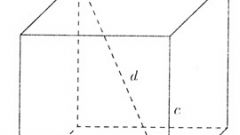
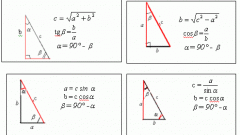
Используйте теорему Пифагора для вычисления длины диагонали (D) прямоугольника, если из условий задачи известны ширина (W) и высота (H) фигуры. Диагональ и две стороны этого четырехугольника, образующие прямой угол напротив нее, создают прямоугольный треугольник, а теорема Пифагора гласит, что квадрат длины гипотенузы в таком треугольнике равен сумме квадратов длин его катетов. В данном случае гипотенузой является диагональ, а это значит, что для нахождения ее длины вам следует найти корень из суммы возведенных в квадрат длины и ширины прямоугольника: D=√(W²+H²).
2
Модифицируйте полученную формулу, если известна длина только одной стороны прямоугольника (например, H) и его площадь (S). Недостающую сторону в формуле, полученной на предыдущем шаге, можно заменить соотношением между площадью и длиной известной стороны. Подставьте это соотношение в формулу: D=√(H²+(S/H)²)=√(H²+S²)/H.
3
Аналогичным способом измените формулу из первого шага, если известны длина одной стороны (H) и длина периметра (P) прямоугольника. Периметр составляют по две длины каждой из сторон фигуры, а это значит, что вместо длины неизвестной стороны в формулу можно подставить выражение (P-2*H)/2 или P/2-H: D=√(H²+(P/2-H)²=√(H²+P²/4-P*H+H²)=√(2*H²+P²/4-P*H).
4
Если в прямоугольник можно вписать окружность, то этот прямоугольник является квадратом, а значит, длина любой его стороны равна диаметру этой окружности (d). Подставьте это значение в формулу из первого шага: D=√(d²+d²)=d*√2.
5
Без теоремы Пифагора можно обойтись в том случае, если известен диаметр описанной около прямоугольника окружности. Это самый простой вариант нахождения диагонали прямоугольника - длина диагонали совпадает с диаметром окружности.