Инструкция
1
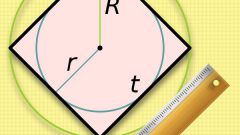
Итак, стоит начать с того, что вокруг квадрата можно описать окружность, диагональ которой в точности равна диагонали квадрата. Для того, чтобы подсчитать радиус описанной окружности, надо воспользоваться формулой:
R = (√2*a)/2, где a - это сторона квадрата.
Также в квадрат можно и вписать окружность. При этом окружность в точках касания ее со сторонами квадрата делит их пополам. Формула, с помощью которой можно вычислить радиус вписанной окружности, выглядит так:
r = a/2
Если, при решении задачи, известен радиус окружности, который вписан в данный квадрат, то возможно таким образом выразить и сторону квадрата, величина которой необходима для нахождения диагонали квадрата:
a = 2*r
R = (√2*a)/2, где a - это сторона квадрата.
Также в квадрат можно и вписать окружность. При этом окружность в точках касания ее со сторонами квадрата делит их пополам. Формула, с помощью которой можно вычислить радиус вписанной окружности, выглядит так:
r = a/2
Если, при решении задачи, известен радиус окружности, который вписан в данный квадрат, то возможно таким образом выразить и сторону квадрата, величина которой необходима для нахождения диагонали квадрата:
a = 2*r
2
Длина радиуса окружности равна половине длины ее диагонали. Таким образом, длина диагонали описанной окружности, а, значит, и длина диагонали квадрата может быть рассчитана по формуле:
d = √2*a
d = √2*a
3
Для большей ясности, можно рассмотреть небольшой пример:
Дан квадрат с длиной стороны 9 см, требуется найти длину ее диагонали.
Решение: для того, чтобы подсчитать ее длину, потребуется воспользоваться формулой выше:
d = √2*9
d = √162 см
Ответ: длина диагонали квадрата со стороной 9 см равна √162 см или, приблизительно, 14.73 см
Дан квадрат с длиной стороны 9 см, требуется найти длину ее диагонали.
Решение: для того, чтобы подсчитать ее длину, потребуется воспользоваться формулой выше:
d = √2*9
d = √162 см
Ответ: длина диагонали квадрата со стороной 9 см равна √162 см или, приблизительно, 14.73 см
Видео по теме
Обратите внимание
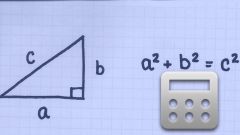
Стоит учесть, что диагональ квадрата делит его на 2 прямоугольных треугольника, которые, помимо всего, еще являются равнобедренными.
Дело в том, что диагональ является гипотенузой одного из двух прямоугольных треугольников. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов его катетов (a² = b² + c²). Тогда длину диагонали a можно найти при помощи формулы:
a = √(b² + c²), где b = c, так как они - равные стороны квадрата.
Дело в том, что диагональ является гипотенузой одного из двух прямоугольных треугольников. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов его катетов (a² = b² + c²). Тогда длину диагонали a можно найти при помощи формулы:
a = √(b² + c²), где b = c, так как они - равные стороны квадрата.
Полезный совет
Нельзя забывать, что квадрат является уникальной геометрической фигурой. Квадрат обладает пятью осями симметрии, четыре из которых являются отражательными осями, а одна - вращательной.
Источники:
- формула диагонали квадрата
- Так как стороны квадрата равны, то он является