Инструкция
1
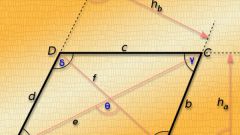
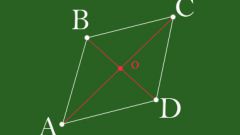
В любой замкнутой геометрической фигуре, состоящей не менее чем из четырех отрезков, можно провести как минимум две диагонали. Именно столько диагоналей может иметь четырехугольник: параллелограмм, прямоугольник, ромб и квадрат.
2
Найдите диагонали параллелограмма, если известно, что одна из них больше другой на 1, а длины сторон равны a=5 и b=7. На этот счет в геометрии есть готовая формула, согласно которой сумма квадратов длин диагоналей равна удвоенной сумме квадратов сторон:d1² + d2² = 2•(a² + b²) = 2•(25 + 49) = 148.
3
Подставьте d2=d1+1:d1² + (d1+1)² = 148 2•d1² + 2•d1 + 1 = 148.
4
Решите следующее уравнение относительно неизвестной d1:2•d1² + 2•d1 – 147 = 0D = 4 + 4•2•147 = 1180d1 = (-2 + √1180)/4 ≈ 8,1 → d2 = 9,1.
5
Формула для прямоугольника упрощается, поскольку его диагонали равны между собой:2•d² = 2•(a² + b²) = 2•(25 + 49) = 148 → d² = 74 → d ≈ 8,6.
6
В случае квадрата дело обстоит еще проще, его диагонали не только имеют равную длину, но и прямо пропорциональны стороне:2•d² = 4•a² → d² = 2•a² → d = √2•a = [a=5] = √2•5 ≈ 7.
7
Ромб – частный случай параллелограмма с равными сторонами, однако в отличие от квадрата диагонали не равны между собой. Предположим, что сторона ромба a=5, а длина одной из диагоналей равна 3. Тогда:d1² + 9 = 4•25 → d1 = 9.
8
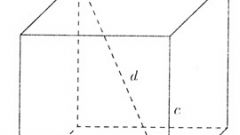
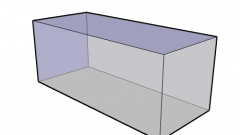
Диагонали можно провести не только в плоской фигуре, но и в пространственной. Например, в параллелепипеде. Квадрат длины диагонали прямоугольного параллелепипеда (или его частного случая - куба) равен суммарной величине квадратов трех его измерений. Измерениями называются ребра, имеющие одну общую вершину.
9
Диагоналей не имеет треугольник и его трехмерный вариант – тетраэдр, поскольку у них отсутствуют несмежные вершины. Количество же диагоналей в любом n-многоугольнике можно определить следующим образом:nd = (n² – 3•n)/2.
Видео по теме